
Stage3DとAGAL2を使ってGPGPUで流体シミュレーションを作ってみました。
元ネタはStable Fluidsです。
>> Open simulation (Required Flash Player 16 or later)
>> View source code
(発散に関する記述を修正しました:2016/02/07)
GPGPU部分は計算を押し付けてるだけなので、先にシミュレーション部分の解説から。
流体の色を記録した色テクスチャと、流体の速度を記録した速度テクスチャを使って
シミュレーションを進めていきます。
何をやっているか?
1.初期化、各種テクスチャを用意する
2.速度の発散を計算する
3.圧力を計算する
4.速度に圧力を適用する
5.色テクスチャと速度テクスチャを更新する
6.色テクスチャを画面に表示する
7.2~6を繰り返す
2~5がメインの計算部分です。まずは5を見てみましょう。
色テクスチャと速度テクスチャの更新
流体の「流れ」を計算する部分です。
色テクスチャの更新はこんな感じで行われます。
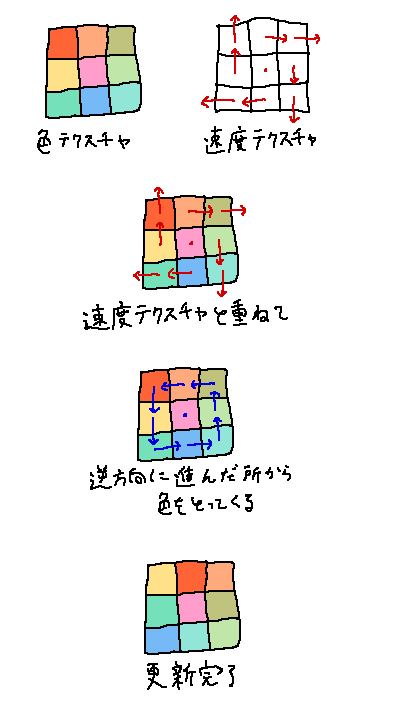
速度テクスチャの更新も色テクスチャと全く同じです。
図は矢印が増えて逆にややこしくなりそうなので割愛。
これでとりあえず流れてくれます。
速度調整の必要性
さて、ただ流れれば流体に見えるかというとそうではありません。
現実の流体は突然どこかから湧き出してきたり、逆にどこかへ消えていくことはありません。
したがって、シミュレーションにおいても流体が湧き出てくるような点や、
吸い込まれていくような点を排除する必要があります。
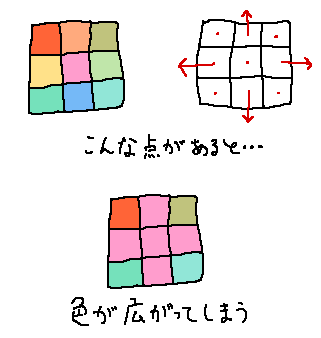
「湧き出し点」の例
2~4の計算はこれらの点を排除するためのものです。
発散について
ベクトル解析には「発散」という概念があります。
これは「ある点から外側の点に向かってどれだけベクトルが放射されているか」
を表すもので、速度ベクトルの発散はまさにさっきの「湧き出し量」に該当します。
ここでは発散がプラスなら湧き出し、マイナスなら吸い込みであるとします。
このときある点での発散は、x軸プラスを右、y軸プラスを下として、
(右の点の速度のx成分) – (左の点の速度のx成分) +
(下の点の速度のy成分) – (上の点の速度のy成分)
で計算できます。
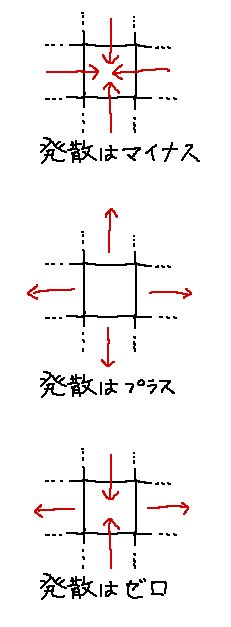
要はすべての点で速度ベクトルの発散がゼロになってくれれば良い訳です。
圧力で発散を打ち消す
ではどうやって発散をゼロにするかですが、
圧力をうまく計算して発散を打ち消すという方法があります。
圧力はそれぞれの点の「反発力」のようなもので、
圧力が大きいほど周囲の点を押し返す力が働きます。
逆にマイナスの圧力は周囲の点を引き寄せる力が働きます。
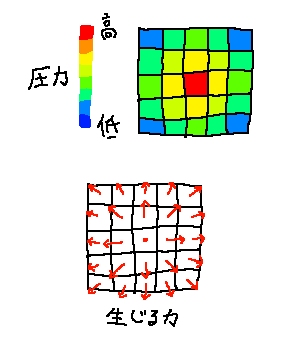
ある点に生じる力は、隣り合う点の圧力の差から計算できます。
(力のx成分) = {(左の点の圧力) – (右の点の圧力)} * 0.5
(力のy成分) = {(上の点の圧力) – (下の点の圧力)} * 0.5
この力をそのまま速度に加えるとすると、※力を撃力とみなし、密度は一様として無視する
圧力の適用による速度変化は次のようになります。
(速度のx成分) += {(左の点の圧力) – (右の点の圧力)} * 0.5
(速度のy成分) += {(上の点の圧力) – (下の点の圧力)} * 0.5
圧力をどう計算するか?
圧力と圧力による速度変化がわかった所で、実際に発散を打ち消す圧力を計算します。
途中計算は省略しますが、ある点に隣り合う4点の圧力が決まっているとき、
中心の点の圧力をpにしたとすると、中心の点の発散は圧力の適用後
4 * p – (左の圧力) + (右の圧力) + (上の圧力) + (下の圧力)
だけ変化します。
変化前の発散をdとすると、これが変化後に0になってほしいので、
-d = 4 * p – (左の圧力) + (右の圧力) + (上の圧力) + (下の圧力)
が成り立つ必要があります。変形すると
p = {(左の圧力) + (右の圧力) + (上の圧力) + (下の圧力) – d} * 0.25
となります。
実際に圧力を計算する
この式を使ってそれぞれの点の圧力を計算します。
ただしこの式は「周囲の点の圧力が確定している」時にしか使えないので、
まともに計算しようとすると巨大な連立方程式を解くことになります。
そこで、この手の計算によく使われる反復法(Gauss-Saidel法など)を利用します。
この場合の反復法とは、
始めに圧力を0など適当な値にセットしておく
セットされた圧力を使って新しい圧力を計算する
計算された圧力を使ってまた新しい圧力を計算する
また計算された圧力を使ってさらに新しい圧力を計算する
・・・
という風に、圧力を繰り返し計算しつつ徐々に精度を上げていく方法です。
この方法は非常に強力で、Box2DやBulletなど各種物理エンジンでも使われています。
まとめ
以上で一通りの説明が終わったので、2~4の流れを確認します。
・テクスチャの各ピクセルに対し、
(左の速度.x) – (右の速度.x) + (上の速度.y) – (下の速度.y)
を計算する。これを各ピクセルの発散とする。
・各ピクセルの圧力を0に設定する。
・各ピクセルに対し、圧力を
{(左の圧力) + (右の圧力) + (上の圧力) + (下の圧力) – (発散)} * 0.25
で更新する。
・↑を何度か繰り返す。
・各ピクセルに対し、
(速度.x) += {(左の圧力) – (右の圧力)} * 0.5
(速度.y) += {(上の圧力) – (下の圧力)} * 0.5
を計算する。
発展
実は反復法を使うときには、Warm Startingという非常に便利な技が使えます。
Warm Startingでは、反復法の最初で値を0にセットする代わりに、
直前に計算した値をセットします。
シミュレーションでは状況が少しずつ変化するので、求める値も少しずつ変化します。
そこで、直前に計算した値から出発して計算することで、反復計算の精度を
格段に上昇させることができるのです。
比較用に、Warm Startingを使わないバージョンを置いておきます。
歴然とした精度の差が分かると思います。
Warm Startingを利用した2~4の流れは以下のようになります。
ほとんど変わっていません。
・テクスチャの各ピクセルに対し、
(左の速度.x) – (右の速度.x) + (上の速度.y) – (下の速度.y)
を計算する。これを各ピクセルの発散とする。
・各ピクセルの圧力を保存された圧力に設定する。
・各ピクセルに対し、圧力を
{(左の圧力) + (右の圧力) + (上の圧力) + (下の圧力) – (発散)} * 0.25
で更新する。
・↑を何度か繰り返す。
・各ピクセルの圧力を保存しておく。
・各ピクセルに対し、
(速度.x) += {(左の圧力) – (右の圧力)} * 0.5
(速度.y) += {(上の圧力) – (下の圧力)} * 0.5
を計算する。
GPGPU化する
適当にシェーダーを書いてテクスチャに描画して計算してください。
浮動小数点テクスチャを利用するといいです。
おわり