粒子法で3Dの弾性体シミュレーションを作りました。
CPUで物理演算、GPUでメッシュの変形を計算します。
>> Run simulation (Required Flash Player 18 or later)
>> View source code
粒子法を使う
弾力のある柔らかい物体をシミュレーションするので、変形をうまく表現できるような手法を選ぶ必要があります。他にもいくつか方法はありますが、扱いが比較的簡単な粒子法を選びました。
物体を細かい粒子に置き換えて、個々の粒子の運動を計算することで物体の動きを計算します。

粒子で表現されたドーナツ状のリング
粒子を繋げる
物体を粒子で置き換えても、そのままでは粒子が繋がっていないのでバラバラに動いてしまいます。

崩壊するリング
そこで、隣り合う粒子間にバネを配置します。フックの法則に従うバネと、安定化のためのダンパを使います。このとき、位置のずれに対するバネだけでなく、角度のずれに対するバネも合わせて配置します。
でないと物体がひものように柔らかくなります。元の形状を記憶できないからです。
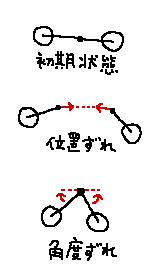
初期状態と位置のずれに対するバネ、角度のずれに対するバネ
角度のずれを計算するためには当然ながら粒子が角度の情報を持っている必要があり、今回は3次元なのでクォータニオンか回転行列が必要になります。回転行列だと姿勢を角速度で更新する際に面倒(誤差が蓄積するのを防ぐために毎回対角化しないといけない)なのでクォータニオンを使いました。この辺は剛体と同じです。
バネを強くする
これまでで一応柔らかい物体の計算はできるようになりましたが、通常の(1/60秒の)時間刻み幅でシミュレーションを実行すると、バネが弱すぎることが分かります。バネ係数を上げればバネは強くなりますが、上げ過ぎるとすぐに発散してしまうのであまり強くすることができません。

うーん、柔らかすぎる……
そこで、バネの計算式を変更して拘束条件と見なし、反復計算を行うことでバネを強化します。元のバネとダンパの式を捨てて、次のような拘束条件を考えます。 \vec{x_1}(t),\vec{x_2}(t) はそれぞれ粒子1, 粒子2の時刻 t におけるバネの接続位置で、 \vec{v_1}(t),\vec{v_2}(t) はそれぞれ粒子1, 粒子2の時刻 t における速度、 \vec{f} は粒子間に働く力、 h は時間刻み幅です。
\begin{aligned}
\vec{x_1}(t+h)=\vec{x_2}(t+h)
\end{aligned}
すなわち
\begin{aligned}
\vec{x_1}(t)+h\vec{v_1}(t+h)=\vec{x_2}(t)+h\vec{v_2}(t+h)
\end{aligned}
ここで、 \vec{x_1}(t)-\vec{x_2}(t) が粒子間の「位置のずれ」を表すものと考えると、この拘束条件は「時刻 t+h には位置のずれが完全に解消されている」ことを表します。超強力なバネ……というかもはやバネじゃないですね。
この式には時刻 t+h における粒子の速度 \vec{v_1}(t+h),\vec{v_2}(t+h) が入っているので、拘束条件を満たさせるために与える力(=拘束力)を求めるためには、 \vec{v_1}(t+h),\vec{v_2}(t+h) を知っておく必要があります。ですが \vec{v_1}(t+h),\vec{v_2}(t+h) の値はこのバネの拘束力だけでなく、粒子が繋がっている別のバネの拘束力によっても変化します。つまり、このバネの拘束力を1回の計算で求めることはできません※1。
※1 巨大な行列の逆行列を計算すればできないこともない……けど実用的ではない。
そこで反復法の出番となります。拘束力を繰り返し更新していくことで、少しずつ真の値に近づけていきます。詳細は省きますが、次のように計算することで時刻 t+h における粒子の速度を求めることができます。
\begin{aligned} (1/m_1+1/m_2)h\vec{f} &= k[(\vec{x_1}(t)+\vec{v\prime_1})-(\vec{x_2}(t)+\vec{v\prime_2})]\\ \vec{v\prime_1}&\gets \vec{v\prime_1}+h\vec{f}/m_1\\ \vec{v\prime_2}&\gets \vec{v\prime_2}-h\vec{f}/m_2 \end{aligned}ここで、 \vec{v\prime_1},\vec{v\prime_2} は粒子の「仮の速度」で、繰り返し計算するにつれてこの値が \vec{v_1}(t+h),\vec{v_2}(t+h) に近づいていきます。 k はバネ定数……というより緩和係数で、この値が小さいほど仮の速度が緩やかに真の速度に近づいていきます。また、 m_1,m_2 は粒子の質量です。仮の速度は \vec{v_1}(t),\vec{v_2}(t) で初期化しておき、全てのバネに対して先程の計算を繰り返し行います。最後に、 \vec{v_1}(t+h),\vec{v_2}(t+h) に仮の速度を代入します。
バネの強さを調節する
先ほどの計算において、緩和係数を上げ、繰り返し回数を増やすほどバネは強くなります。逆に言えば、バネの強さを緩和係数と繰り返し回数によって調節することができるということです。いろいろ試してみて、丁度いい硬さになるパラメーターを探してやりましょう。
いくつか繰り返し回数を変えて計算した結果をキャプチャしてみました。

繰り返し回数:1

繰り返し回数:3

繰り返し回数:5

繰り返し回数:20
さすがに1回だとでろんでろんになって、3~5回がいい感じ、20回だとほとんど変形しなくなりました。今回は5回の繰り返しを採用することに。
本当はバネの硬さだけでなく、減衰具合(低いほど物体がぷるぷるする)も調節したいところでしたが、残念ながらこの拘束モデルではうまく調整できませんでした。ちゃんとやろうとすると Soft Constraints のような計算方法が必要になりそうです。今回のはなかなか手軽でお気に入りなのですが……
メッシュを変形させる
さて、今まで描画を粒子のまま行ってきましたが、これをメッシュで描画する方法を考えます。粒子の移動・回転に合わせてメッシュを滑らかに変形させつつ描画します。3Dモデルであるメッシュも頂点の集まりでできているので、頂点をうまく動かしてやればOKです。
パッと思いつく方法は、メッシュのそれぞれの頂点に対し、初期状態で最も近い粒子を記憶させ、その粒子に合わせて頂点を移動させる方法です。初期状態での粒子から頂点への相対位置を求めておき、それを回転させたものに粒子の座標を加えることで現在の頂点の座標を求めます。
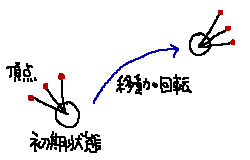
一番近い粒子に頂点を「貼り付ける」イメージ
この方法はそこそこうまく行きますが、物体が大きく変形したときにメッシュが滑らかにならないという問題点があります。これは最も近い粒子だけの情報を使っているためです。

持ち手の部分や注ぎ口の根元がいびつになっている
そこで、適当な重み関数を用いて複数の粒子から求めた頂点座標の重み付き平均をとってやります。今回は3粒子の重み付き平均をとりましたが、大きな変形でも滑らかにメッシュが変形するようになりました。

持ち手や注ぎ口の根元も滑らかに変形している
頂点の移動は行列を掛けるだけでできるので、頂点シェーダを書いてGPU側で処理させると高速化できます。
その他
・粒子同士の衝突は、粒子の半径が同じであることを利用して空間をグリッド分割すると高速に検出できます。粒子を剛体球と見なせば衝突は拘束条件として書けるので、反復計算の中に組み込むことができます。
・影を付けました。一般的なシャドウマップ+ぼかし処理を加えています。地面との距離が大きいほど影がぼけるようにしました。

そういえば
lo-th さんが移植してくれたOimoPhysicsのJavaScript版であるOimo.jsが、知らない間にすごく有名になっていた……! もはや本家のAS3版より圧倒的にJS版の方が人気ですw (thank you lo-th :D)
実はOimoPhysicsですが、実装したかった機能がいくつかあるまま開発が中断してしまっていたので、プラットフォームをAS3からHaxeに変えて書き直そうと思っています。HaxeからはJSにも書きだせるので、JS版のアップデートもされることになります。しばらく集中的に取り組もうと思っているので、乞うご期待!
