SPH法とMPS法で流体シミュレーションしてみました。ついでにリアルタイム計算向けの手法を考えました。
デモは加速度センサーに対応しているので、スマートフォンから見ると面白いかもしれません。
* この記事は rogy Advent Calendar 2017 の記事です
※注:記事の続きにはgif動画が10個くらい貼ってあるので、全部読み込むと結構な通信量になります。一応注意してください。
もくじ
超長いので目次です。
粒子法について
粒子法は、連続体を複数の粒子に分解し、粒子の上で計算を進めることで元の連続体の動きをシミュレートする手法です。格子法と異なり、粒子自体が位置を持ち、そして「動く」ことができるので、流体の細かい水しぶきや弾性体の大きな変形を扱うのに適しています。
一口に粒子法と言っても色々な手法があり、それぞれ性質や適している計算対象が異なります。ここでは流体を計算対象として、SPH (Smoothed Particle Hydrodynamics) 法 と MPS (Moving Particle Semi-implicit) 法 を紹介します。
粒子法の難しさ
格子法に比べて、粒子法によるシミュレーションは一般に難しいのではないかと思っています。例えば、格子法ではベクトル演算 \mathrm{(grad,div,rot)} に対しある程度自然な離散化※1連続体は数式上では無限の細かさを持ちますが、コンピューターで計算できるのは有限の細かさです。無限の細かさを持つものを有限の細かさに落とし込むことを離散化と言います。方法が存在しますが、粒子法では自明な離散化方法がありません。そのため、まず離散化方法からして慎重に検討する必要があります。実際、SPH法とMPS法では異なる離散化方法を採用しており、これらの違いによってある条件下での挙動が全く違ったものになることがあります。
実際は、手法ごとに離散化方法が提示されているのでその部分で悩む必要はありませんが、その意味を理解し、正しくプログラムに落とし込むのが非常に難しいです。
ここではSPH法, MPS法の離散化の考え方や実装上の注意点を解説します。できるだけ分かりやすく解説するつもりではありますが、ベクトル解析・偏微分・積分などの知識は暗黙のうちに使うことがあります。
共通する考え方
SPH法とMPS法に共通する考え方として、ある点における連続体の物理量※2物体が持つ物理的なパラメータのことを物理量と言います。例えば速度、温度、質量などは物理量です。を、周辺の粒子の物理量の重み付き和で表現するというものがあります。例えば、ある点における温度は、周辺の粒子の温度の重み付き和で求めます。こうすることで、元の連続体上の物理量を滑らかに粒子間で補間することができるようになります。
まず「周辺の粒子」について、どこまでを「周辺」とするのかが問題となります。無限遠方まで考えるのは現実的ではないので、ある半径 r_e を定め、その半径以内にいる粒子のみを「周辺にいる」粒子と見なします。この半径 r_e のことを影響半径と言います。
次に、周辺の粒子の物理量をどのようにして重み付けするかが問題になります。直感的に、近い位置にいる粒子に大きな重みをおき、遠く(=影響半径近く)にいる粒子に小さな重みをおくべきなのは分かると思います。このように距離に対して重みを定めたもの(=重み関数)をカーネルと言います。
以上の「物理量の平滑化」「影響半径」「カーネル」という考え方は、SPH法とMPS法で共通しています。しかしながら、その細かい定義や使われ方はSPH法とMPS法で異なってきます。
SPH法での物理量の近似
まずはSPH法について、物理量の近似手法を詳しく見ていきます。
SPH法では、位置 x における物理量 \phi(x) を次のように空間で積分して近似します。積分範囲はシミュレーションの次元に合わせて考えてください(2次元なら \mathbb R^2 、3次元なら \mathbb R^3 など)。
\begin{aligned}
\phi(x)\approx\int\phi(r)W(x-r)dr
\end{aligned}
右辺の \phi(r) は重み付けされる前の物理量であることに注意してください。後でこの部分が粒子の物理量に置き換わります。
W は正規化されたカーネルです。ここでの正規化とは「空間全体にわたって積分すると値が1になる」という意味で、数式で表すと次のようになります。
\begin{aligned}
\int W(x-r)dr=1
\end{aligned}
最初の積分が \phi(r) の重み付き平均になっているのが分かるでしょうか。
このままでは物理量が「無限の細かさ」を持つ積分で書かれているため、これをそのまま計算することはできません。そこで、右辺の物理量の積分を有限個の粒子の物理量の和で近似します。具体的には、粒子1つのもつ体積 \Delta r を決めてやり、 \phi(r)dr を \phi_j\Delta r で近似します。ただし、 \phi_j は粒子 j のもつ物理量です。
\begin{aligned}
\int\phi(r)W(x-r)dr\approx\sum_j\phi_j\Delta rW(x-x_j)
\end{aligned}
ここまでは比較的分かりやすいかと思います。しかし、SPH法では粒子の体積 \Delta r を直接利用しません。代わりに、粒子 j のもつ質量 m_j と、粒子 j が表す物質の密度 \rho_j を使った式を使います※3なんでこうするかは知りませんが、ほとんどの文献でこうなっています。詳しい理由を知っている方がいたら教えてください。。最終的に、物理量 \phi(x) は次のように求められます。
\begin{aligned}
\phi(x)=\sum_j m_j\frac{\phi_j}{\rho_j}W(x-x_j)
\end{aligned}
これで、粒子に与えられた物理量からある位置における物理量を求めることができるようになりました。
Navier-Stokes方程式
ところで、今回計算する流体の運動方程式は次のようなものです。
\begin{aligned}
\frac{Dv}{Dt}=-\frac1\rho\nabla p+\nu\nabla^2v+g
\end{aligned}
これだけでも十分複雑そうに見えますが、元のNavier-Stokes方程式はとんでもない形をしているため、密度一定・粘性一定を仮定して単純化されたものを使っています。以下では、この式の直感的な意味を解説します。
\begin{aligned}
\frac{Dv}{Dt}
\end{aligned}
は速度 v のラグランジュ微分を表します。速度のラグランジュ微分とはなんぞや、というと、流体とともに流れている視点から見たときの速度変化です※4ちなみに、止まっている視点から見た速度変化のことを速度のオイラー微分と言いますが、今回は出番がありません。。粒子法では粒子そのものが流体の流れを表すので、これは粒子から見た速度変化、すなわち粒子の速度変化であると言えます。
\begin{aligned}
-\frac1\rho\nabla p
\end{aligned}
は圧力項といい、圧力 p による粒子の速度変化を表します。満員電車の中にいる密度 \rho の自分を想像してみてください。 \nabla p は圧力の勾配といい、圧力が最も大きくなる方向を向いたベクトルで、大きさは圧力の変化率に比例します。例えば、左にいる人の圧力が高く、右にいる人の圧力が低ければ \nabla p は左を向きます。ところがこのとき実際に力がかかるのは右の方向です。なのでマイナスが付いているのです。自分が重いほどかかった力に対する速度変化は小さくなりますから、 1/\rho が掛けられます。
\begin{aligned}
\nu\nabla^2v
\end{aligned}
は粘性項といい、粘性による粒子の速度変化を表します。 \nu は動粘性係数※5粘性係数 \mu を密度 \rho で割ったものです。で、粘性の強さを表します。ところで粘性とはどういうものでしょう。粘性の高い流体はドロドロしているわけですが、これは流体の内部に摩擦力のようなものが働いている、と考えることができます。摩擦力は「速度のずれを無くそうとする力」であり「自分の速度を周りの速度に近付ける力」です。 \nabla^2v は速度 v のラプラシアンといい、簡単な説明が難しいのですが、周りの平均の速度と自分の速度の差のようなものを表します。つまり、自分の速度に \nabla^2v を足すことで、自分の速度は周りの平均的な速度に近付いていきます。 \nu が大きいほど周りの速度により速く近付くようになるのは容易に想像がつくと思います。
\begin{aligned}
g
\end{aligned}
は外力項といい、外的な要因で働く力による速度変化を表します。文字から想像がつくと思いますが、例えば重力などがこれにあたります。
それでは、この方程式に従ってSPH法で流体をシミュレートする方法を見ていきましょう。
SPH法における空間微分
先程のNavier-Stokes方程式には空間微分演算子※6時間 t ではなく、空間の座標軸 e_x,e_y,e_z に沿った偏微分を行う演算子のことです。である \nabla が入っていましたが、SPH法では物理量の空間微分をカーネルの空間微分にすり替えます。位置 x での物理量 \phi(x) は
\begin{aligned}
\phi(x)=\sum_j m_j\frac{\phi_j}{\rho_j}W(x-x_j)
\end{aligned}
で与えられましたが、右辺において x が直接(陽に)関係する項は W(x-x_j) のみです。したがって、 \phi(x) の勾配 \nabla\phi(x) は
\begin{aligned}
\nabla\phi(x)=\sum_j m_j\frac{\phi_j}{\rho_j}\nabla W(x-x_j)
\end{aligned}
であると考えることができます。
\phi(x) のラプラシアンも同じように求めることができます。
\begin{aligned}
\nabla^2\phi(x)=\sum_j m_j\frac{\phi_j}{\rho_j}\nabla^2W(x-x_j)
\end{aligned}
このようにSPH法では、物理量の空間微分を、重み関数 W を \nabla W や \nabla^2W に変えるだけで計算できます。
別の導出方法
これは余談なので読み飛ばしてもらって構わないのですが、先程の式は空間微分された物理量の重み平均
\begin{aligned}
\int\nabla\phi(r)W(x-r)dr
\end{aligned}
からも導出できます。
部分積分の公式を用いて
\begin{aligned}
\int\nabla\phi(r)W(x-r)dr&=\int\nabla\left(\phi(r)W(x-r)\right)dr+\int\phi(r)\nabla W(x-r)dr\\
&=\int_S\phi(r)W(x-r)dS+\int\phi(r)\nabla W(x-r)dr\\
&=\int\phi(r)\nabla W(x-r)dr
\end{aligned}
2行目でストークスの定理を使って体積分を面積分に置き換えています。カーネル W は遠方で0となるので、面積分はそのまま0になり、結局カーネルだけ微分すればよいことが分かります。発散やラプラシアンについても同様に導くことができます。
Navier-Stokes方程式の離散化
これで流体を計算する準備ができたので、Navier-Stokes方程式の右辺の圧力項、粘性項、外力項を計算できる形に離散化します。
\begin{aligned}
\frac{Dv}{Dt}=-\frac1\rho\nabla p+\nu\nabla^2v+g
\end{aligned}
計算を進める上で、このままの形では扱い辛いので式を少し変形します。
\begin{aligned}
\rho\frac{Dv}{Dt}&=f^{press}+f^{visc}+f^{ext}\\
f^{press}&=-\nabla p\\
f^{visc}&=\mu\nabla^2v
\end{aligned}
動粘性係数 \nu が粘性係数 \mu に、外力による速度変化 g が外力 f^{ext} に変わっていることに注意してください。
さらに、時間刻み幅 \Delta t を使って各粒子 i に対する速度の更新式に書き換え、空間微分を離散化します。
\begin{aligned}
v_i^{t+\Delta t}&=v_i^t+\Delta t\frac1{\rho_i}\left({f_i^{press}+f_i^{visc}+f_i^{ext}}\right)\\
f_i^{press}&=-\sum_j m_j\frac{p_j}{\rho_j}\nabla W(x_i-x_j)\\
f_i^{visc}&=\mu\sum_j m_j\frac{v_j}{\rho_j}\nabla^2W(x_i-x_j)
\end{aligned}
後はこの通りに計算するプログラムを書けば完成・・・のはずなのですが、問題点があります。それは、粒子間に働く力が対称でないということです。ニュートンの法則に従えば、2粒子間に働く力は必ず同じ大きさで正反対の方向を向いていなければなりません。そこで、まず圧力項 f_i^{press} を次のように修正します。
\begin{aligned}
f_i^{press}=-\sum_j m_j\frac{p_i+p_j}{2\rho_j}\nabla W(x_i-x_j)
\end{aligned}
これこんなことして大丈夫なのか?という疑問がありますが、大域的に見ると合計値は変わっていないので恐らく大丈夫なのでしょう。粒子法では「粒子の大きさと影響半径を0に近付ければ厳密な解に近付くのでOK」という考え方をすることが多いです。
また、粘性項についても粒子間の力が非対称になっているので、次のように速度の差を取った式を使います。
\begin{aligned}
f_i^{visc}=\mu\sum_j m_j\frac{v_j-v_i}{\rho_j}\nabla^2 W(x_i-x_j)
\end{aligned}
これについても大丈夫なのかという疑問がわきますが、粒子が均等に存在しているという仮定の下では元の式と等しくなります。粒子が均等に存在している場合、対称性より
\begin{aligned}
\sum_j \frac{m_j}{\rho_j}\nabla^2 W(x_i-x_j)=0
\end{aligned}
が成り立つはずであり※7この式は「定数スカラー場 1 のラプラシアン」を意味します。、 v_i の関係する部分が0になってくれます。
圧力をどうするか
実は上の式はまだ計算することはできません。式中に出てくる圧力 p の値が分からないからです。格子法では、圧力を求めるために連続の式とよばれる方程式
\begin{aligned}
\nabla\cdot v=0
\end{aligned}
を用いて圧力を決定します。連続の式を使うと、Poisson方程式とよばれる圧力の連立方程式が出てくるので、それを解くことで圧力が計算できます(ここにやや詳しく書いてあります)。この方法を使うと、非圧縮性の流体をシミュレートすることができます。
しかし、SPH法では連続の式を使いません。代わりに、圧縮性の理想気体の状態方程式に似た以下のような式を使って圧力を決定することが多いです。
\begin{aligned}
p_i=k(\rho(x_i)-\rho_0)
\end{aligned}
ただし、 \rho(x_i) は、次の式を使って求めます。
\begin{aligned}
\rho(x_i)=\sum_j m_j W(x_i-x_j)
\end{aligned}
ここで、 \rho_0 は粒子の初期配置(=安定している状態)における密度です。密度が高くなったら圧力を上げて粒子を反発させ、元の密度 \rho_0 に戻そうとします。この式は連立方程式ではないので、一度の計算で(=陽的に)圧力を求めることができます。
しかし、この方法を使うと完全な非圧縮性流体が計算できないので、適当に k の値を大きくして非圧縮性を高めてやります。ただし、 k を大きくしすぎると爆発するのでその辺は注意してやる必要があります※8 k の値を大きくするほど、安全に(爆発せずに)計算できるタイムステップ幅 \Delta t が小さくなります。安全に計算できるタイムステップ幅を評価する方法もありますが、ここでは割愛します。。
また、この式を使って圧力を計算した場合、粒子数の少ない界面付近で負圧が発生し、粒子が凝集してしまい計算が不安定になることがあります。これを避けるため、 p_i が負になった場合は p_i=0 としてやります。
SPH法の重み関数
今までカーネル W が出てきましたが、SPH法では3種類のカーネルを使い分ける方法が一般的なようです。以下のカーネルは、いずれも |r|\gt r_e の場合は値を0にします。
まず、密度計算に使うカーネル W_{poly6} です。このカーネルは、 \rho(x_i) を求めるときの重み関数として使います。
\begin{aligned}
W_{poly6}(r)&=a(r_e^2-|r|^2)^3\\
a&=\begin{dcases}
\frac{4}{\pi r_e^8}&(2D)\\
\frac{315}{64\pi r_e^9}&(3D)
\end{dcases}
\end{aligned}
2次元の場合と3次元の場合で正規化のための定数 a が異なることに注意してください※92次元だと積分範囲が円になり、3次元だと積分範囲が球になるためです。。
次に、圧力計算に使うカーネル W_{spiky} です。このカーネルは、圧力の勾配 \nabla p を求めるときの重み関数として使います。
\begin{aligned}
\nabla W_{spiky}(r)&=a(r_e-|r|)^2\frac{r}{|r|}\\
a&=\begin{dcases}
-\frac{30}{\pi r_e^5}&(2D)\\
-\frac{45}{\pi r_e^6}&(3D)
\end{dcases}
\end{aligned}
最後に、粘性項の計算に使うカーネル W_{visc} です。このカーネルは、速度のラプラシアン \nabla^2 v を求めるときの重み関数として使います。
\begin{aligned}
\nabla^2W_{visc}(r)&=a(r_e-|r|)\\
a&=\begin{dcases}
\frac{20}{3\pi r_e^5}&(2D)\\
\frac{45}{\pi r_e^6}&(3D)
\end{dcases}
\end{aligned}
SPH法のカーネルに関しては、さらに詳しい解説が SPH法の重み関数 に載っているので、詳しく知りたい方はそちらを参照してください。
壁粒子
このままでは地面や壁などの計算ができませんが、壁粒子を配置することで地面や壁を再現することができます。壁粒子には通常の粒子とほとんど同じ計算を行いますが、速度を常に0に固定します。外力によって位置が固定されていると考えてもいいでしょう。このような壁粒子を3~4層分(影響半径以上の厚みをもつように)配置してやります。
動かしてみた
以上を基に、2次元のSPH法を実装して動かしてみました。流体は水を想定し、密度を 1000\mathrm{kg/m^2} (???)、粘性係数を 0.001\mathrm{Pa\cdot s} 、初期配置の間隔を 0.025\mathrm{m}=2.5\mathrm{cm} 、影響半径をその 2.5 倍としてあります。時間刻み幅は 1/5000\mathrm{s} です。

はい、うまくいきません。粒子の並びが乱れ始めたあたりから挙動がおかしくなり、最終的に気体分子のごとく空間を飛び回ります。時間刻み幅や圧力の係数 k をいろいろ変更して試してみましたが、遅かれ早かれこんな感じの挙動になります。
粘性の影響はシーンのスケールが大きくなるほど小さくなる上に、粒子法では格子法と違い移流による数値粘性が発生しないため、粘性の影響が小さくなりすぎているようです。ならばと思い、粘性係数を10000倍にしてみました※10こうなるともはや水ではないですが、元々水の粘性が小さいため、そこまで非現実的な値でもないはずです。。

多少マシにはなりましたが、粒子が跳ね回るという結末は変わらないようです。
散々頭を抱えた結果、密度計算に使用した W_{poly6} が悪いのではという結論に辿り着きました※11 W_{poly6} カーネルは r=0 付近で値が一定になり、粒子の距離に対する値の変化が鈍くなります。このため圧力計算では W_{spiky} を使ったのですが、同じ問題が密度計算でも現れているのではないか、という推測です。。そこで、密度計算にも圧力計算と同じ W_{spiky} を使ってみることにしました。
\begin{aligned}
W_{spiky}(r)&=a(r_e-|r|)^3\\
a&=\begin{dcases}
\frac{10}{\pi r_e^5}&(2D)\\
\frac{15}{\pi r_e^6}&(3D)
\end{dcases}
\end{aligned}

今度はうまく動きました!
一連の動画は60FPSで計算した結果を20倍速にしていますが、それでもスロー再生状態になっているので、もう少し解像度を上げて実時間まで早回しにした動画を載せておきます。

まとめ(SPH法)
一応それらしく動かすことには成功しましたが、やはりそのままのSPH法はリアルタイム計算には向かないなという印象でした。1タイムステップあたりの計算時間は高速なのですが、十分な非圧縮性を確保しようと思うとタイムステップ幅をかなり小さくとらないといけません。ゲーム等で使う場合は、非圧縮性を諦めて大きめのタイムステップ幅で計算するか、SPH法から派生した様々な手法を使うことになるかと思います。
MPS法
続いてはMPS法です。これも全部書いていると大変なので、SPH法と異なる部分をメインに解説します。
MPS法の重み関数
SPH法では3種類の正規化された重み関数を使いましたが、MPS法では1種類の正規化されていない重み関数 w を使います。また、 w の引数はベクトルではなくスカラーとなります。
\begin{aligned}
w(r)&=\frac{r_e}{r}-1
\end{aligned}
MPS法の重み関数についても、 r\gt r_e の場合は値を0にします。また、 r=0 で w(r)=\infty となるため、粒子 i の近傍粒子を用いた計算をする際には、粒子 i 自身は無視して考えます。
MPS法で重要な物理量に、粒子数密度 n があります。これは粒子の密集具合を示すものであり、次の式で計算されます。
\begin{aligned}
n_i=\sum_{j\neq i}w(|x_i-x_j|)
\end{aligned}
MPS法で使うカーネル w は正規化されていないため、同じ配置でも影響半径 r_e の値によって粒子数密度が大きく変化します。そこで、初期配置における粒子数密度の最大値 n^0 を計算しておき、 n_i と n^0 の比を見ることによって粒子 i の圧縮具合を評価します。
MPS法における空間微分
SPH法では物理量を積分の近似で定義し、それを微分することで勾配や発散などの計算を行いましたが、MPS法では微分演算ごとにモデルを用意し、そのモデルに従い微分演算を離散化します。
つまり、MPS法ではカーネルを微分せず、空間微分は全て粒子間相互作用の重み付き平均で求めます。これにより、SPH法で問題となった力の非対称性が未然に防がれます。
まず、2粒子 i,j 間における物理量 \phi の勾配 \nabla\phi を次のようにモデル化します。
テイラーの定理を用いて、粒子 i の物理量 \phi_i と粒子 j の物理量 \phi_j 、粒子 i の位置における物理量の勾配 \nabla\phi の関係を記述します。
\begin{aligned}
\phi_j=\phi_i+\nabla\phi\cdot(x_j-x_i)+O(|x_j-x_i|^2)
\end{aligned}
O(|x_j-x_i|^2) を無視すると、
\begin{aligned}
\nabla\phi\cdot(x_j-x_i)&=\phi_j-\phi_i
\end{aligned}
両辺を |x_j-x_i| で割り、単位方向ベクトル \dfrac{x_j-x_i}{|x_j-x_i|} を掛けると
\begin{aligned}
\left(\nabla\phi\cdot\frac{x_j-x_i}{|x_j-x_i|}\right)\frac{x_j-x_i}{|x_j-x_i|}&=\frac{(\phi_j-\phi_i)(x_j-x_i)}{|x_j-x_i|^2}
\end{aligned}
ここで左辺をよく見ると、勾配 \nabla\phi の x_j-x_i 方向の射影ベクトルになっていることが分かります。空間の次元を d とすると、 d 次元から 1 次元に射影したことにより、情報量が 1/d になっています。したがって、この値を d 倍しながら近傍粒子間で重み平均をとることで、元々の勾配が求まりそうです。以上より、粒子 i の位置における物理量の勾配 \nabla\phi_i は次のように計算できます。
\begin{aligned}
\nabla\phi_i = \frac{d}{n^0}\sum_{j\neq i}\frac{(\phi_j-\phi_i)(x_j-x_i)}{|x_j-x_i|^2}w(|x_j-x_i|)
\end{aligned}
カーネル w が正規化されていないため、重み平均をとるために初期配置における粒子数密度 n^0 で割っていることに注意してください。
続いてベクトル値の物理量 u の発散 \nabla\cdot u ですが、これも同様に2粒子間で考えてから重み平均をとることで、次のように計算できます。
\begin{aligned}
\nabla\cdot u_i=\frac{d}{n^0}\sum_{j\neq i}\frac{(u_j-u_i)\cdot(r_j-r_i)}{|x_j-x_i|^2}w(|x_j-x_i|)
\end{aligned}
最後にラプラシアン \nabla^2\phi です。粘性項に出てきたラプラシアンが速度を均一化させていたように、ラプラシアンは物理量の拡散を表します。よって、近傍粒子間で物理量を分け合うような相互作用モデルを考えてやります。
\begin{aligned}
\frac{d}{n^0}\sum_{j\neq i}(\phi_j-\phi_i)w(|x_j-x_i|)
\end{aligned}
しかし、 w の広がり方は影響半径によって異なるため、このままではラプラシアンとして正しく機能しません。そこで、係数 \lambda を導入して、時間経過に対する分散の増加率が拡散方程式
\begin{aligned}
\frac{\partial\phi}{\partial t}=\nabla^2\phi
\end{aligned}
の解と等しくなるようにします。最終的なラプラシアンモデルは以下のようになります。
\begin{aligned}
\nabla^2\phi_i&=\frac{2d}{\lambda n^0}\sum_{j\neq i}(\phi_j-\phi_i)w(|x_j-x_i|)\\
\lambda&=\frac{\sum_{j\neq i}|x_j-x_i|^2w(|x_j-x_i|)}{\sum_{j\neq i}w(|x_j-x_i|)}
\end{aligned}
\lambda は初期配置において一度計算しておけば、その後は使い回すことができます※12ただし、流体の十分内部にある粒子、具体的には影響半径内全体に粒子が均等に存在するような粒子に対して計算しておく必要があります。界面付近の粒子で計算すると値が小さくなってしまうためです。。
非圧縮性流体計算
MPS法では、SPH法と違い非圧縮性流体を計算することができます。SPH法の場合「密度に基準値からのずれが生じたら、それを戻すように圧力を高める」という方法で非圧縮性をある種近似していましたが、MPS法では「密度に基準値からのずれが生じないように圧力を逆算する」という方法で非圧縮性を保ちます※13これは、時刻 t+\Delta t における圧力を求めるのに時刻 t+\Delta t における圧力が必要であることを意味します。このような計算方法を「陰解法」( \leftrightarrow 陽解法)といいます。MPS法のSは “Semi-implicit” の頭文字であり、圧力計算のみに陰解法が使われることを意味しています。。
SPH法では密度 \rho を一定に戻すように圧力を決めましたが、MPS法では粒子数密度 n を一定に保つように圧力を決定します。具体的には、次のような手順で1ステップの計算を行います。
- 粘性項・外力項を計算し、次の時刻の粒子の仮の速度 v^* と仮の位置 x^* を求める
- 仮の位置 x^* における粒子数密度 n^* を求める
- 粒子数密度 n^* を n^0 に補正する圧力 p を求める
- 圧力 p を用いて圧力項を計算し、次の時刻の真の速度 v と真の位置 x を求める
3. における圧力 p の計算が鍵です。目的の p を求めるために、 p による補正後の粒子数密度がどうなるか考えましょう。圧力による速度の補正量 v'=v-v^* と位置の補正量 x'=x-x^* は
\begin{aligned}
v'&=-\Delta t\frac{\nabla p}{\rho}\\
x'&=\Delta tv'\\
&=-\Delta t^2\frac{\nabla p}{\rho}
\end{aligned}
です。一方、質量保存則
\begin{aligned}
\frac{D\rho}{Dt}+\rho\nabla\cdot v=0
\end{aligned}
および、密度が粒子数密度に比例することより、粒子数密度の補正量 n'=n-n^* は
\begin{aligned}
n'&=-\Delta t n^*\nabla\cdot v'\\
&=\Delta t^2\frac{n^*}{\rho}\nabla^2p
\end{aligned}
となります。補正後の粒子数密度 n が n^0 になってくれればよいので、 n'=n^0-n^* と合わせて p について解くと次のような式になります。
\begin{aligned}
\nabla^2p=\frac{\rho}{\Delta t^2}\frac{n^0-n^*}{n^*}
\end{aligned}
これをMPS法のラプラシアンモデルで離散化すると、圧力 p に関する次の連立一次方程式を得ます。
\begin{aligned}
\frac{\rho_i}{\Delta t^2}\frac{n^0-n^*_i}{n^*_i}=\frac{2d}{\lambda n^0}\sum_{j\neq i}(p_j-p_i)w(|x_j-x_i|)
\end{aligned}
解きます。
解き方はJacobi法でもGauss-Seidel法でも共役勾配法でも何でもいいですが、直接解こうとすると行列式が0であるため爆発します(そもそも係数行列が大きすぎるため現実的ではありませんが)。
4. で計算した圧力を適用する際にも注意が必要です。MPS法の勾配モデルに従いそのまま圧力項を離散化すると、SPH法のときと同じように界面付近で挙動が不安定になります。というか即座に爆発します……
SPH法の場合は p が 0 を下回ったら 0 にすることでこの問題を回避できましたが、MPS法の勾配モデルではこの方法ではうまく行きません。代わりに次のように修正した勾配モデルを使用します。
\begin{aligned}
\nabla p_i&=\frac{d}{n^0}\sum_{j\neq i}\frac{(p_j-\hat p_i)(x_j-x_i)}{|x_j-x_i|^2}w(|x_j-x_i|)\\
\hat p_i&=\min_{j\in N_i}\{p_j\}
\end{aligned}
\hat p_i は「 i 自身を含めた i の近傍粒子の中の圧力の最低値」です。これで粒子間に引力が働かなくなる※14式中の (p_j-\hat p_i) が常に非負になるためです。ので、界面付近でも動きが安定します。
壁粒子
壁粒子は、基本的にSPH法と同じように配置します。ただし、後述する境界条件の設定のため、壁の表面上(1層分)にある粒子と壁の内部にある粒子を区別できるようにしておきます。
境界条件と壁粒子
先程の p に関する方程式は、界面上(=境界上)でどのような値をとるかを決めないと値が定まりません。境界上に定める条件のことを「境界条件」といいます。MPS法では、界面を2種類に分け、それぞれに異なる境界条件を設定します。
まず、気液界面、すなわち空気と接している部分の粒子に p=0 の条件を課します※15このように、直接解の値を定める境界条件のことをDirichlet境界条件といいます。。これにより、気液界面での圧力が強制的に0になります。界面上にある粒子 i の判定は n_i<\alpha n^0 で行います( \alpha=0.95 あたりがいい感じです)。界面上にあると判定された粒子の圧力は常に 0 で固定し、値を更新しません。
次に、壁に接している部分の界面に、 s を界面の法線ベクトルとして \nabla p\cdot s=0 の条件を課します※16このように、解の境界に垂直な方向の勾配を定める境界条件のことをNeumann境界条件といいます。。これは、壁の表面上で壁に垂直な方向に速度変化が起こらないことを意味しています。この境界条件を実現するためには、 p の方程式から壁の内部にある粒子を除外してやります※17圧力勾配0のNeumann境界条件は、直感的には、方程式を解く際に粒子 i に隣接する壁の内部の粒子に、粒子 i の圧力をコピーすることで実現できます。しかし、これは壁の内部の粒子を方程式から除外することに等しくなります。。
動かしてみた
以上を基に、MPS法で流体シミュレーションを行いました。流体はまた水を想定して、密度を 1000\mathrm{kg/m^2} (???)、粘性係数を 0.001\mathrm{Pa\cdot s} 、初期配置の間隔を 0.025\mathrm{m}=2.5\mathrm{cm} 、影響半径をその 2.0 倍(SPH法のときは 2.5 倍)としてあります。時間刻み幅は 1/600\mathrm{s} (SPH法のときは 1/5000\mathrm{s} )です。

ええ感じや~~と思っていたら突如爆発しました。
どうやら、自由表面にあると判定されていた粒子が、流体内部にいると判定されるようになった瞬間に圧力が急上昇して飛び散り、それが高速で流体内部に飛び込んだことが引き金となって爆発した模様です。
MPS法で使うカーネルは、距離が 0 になると発散して \infty になるためこういう現象が起きます。
影響半径を大きくしたり時間刻み幅を小さくしてみたりしましたがあまり改善せず、仕方ないので粒子の移動速度に制限をかけることにしました。

爆発しなくなったので良しとします。
SPH法と同じように解像度を上げて早回しにしたものも置いておきます(粘性を500倍に上げました)。

水面がモコモコしているのが謎ですが、もう少し粘性を上げると鎮まるかもしれません。
まとめ(MPS法)
気を抜くと突然爆発することを除けば、SPH法より安定して計算できる+非圧縮性を保証できるあたりが強みな感じがします。
ただ、カーネルの形が危険すぎるのと、SPH法と違い2粒子が接近した場合に圧力が働かなくなる※18局所的に2粒子しか存在しない場合、MPS法の勾配モデルではどう頑張っても圧力の勾配が0になります。ため、これもゲーム向きではなさそうです。というかゲーム以外でも問題になりそうな気がするんですが、解析目的で使っている人はどうしてるんでしょうか……
詳しい人がいたらぜひ教えてください。
追記:コメントより匿名で
・近づきすぎた粒子に対しては非弾性衝突処理を行う
・完全な非圧縮性ではなく微小な圧縮を仮定する
ようにすると計算がうまく進むというアドバイスを頂きました。ありがとうございます。
リアルタイム計算・ゲーム向けの粒子法を開発しよう
というわけで本題です。SPH法とMPS法はリアルタイム計算やゲームへの利用にそれぞれ難点があることが分かりました。
リアルタイム計算向けの手法は、以下のような性質をもつべきです。
・圧縮しない(MPS○、SPH△)
・(多少の不都合が生じても)爆発しない(MPS×、SPH○)
・ある程度大きな時間刻み幅で計算できる(MPS△、SPH×)
SPH法とMPS法をいい感じに組み合わせればこれらを満たす手法が作れそうですね。では作ってみましょう。
作ってみた
作りました。MPS法の最初の動画と同じ条件で動かしたものが次です。ただし、時間刻み幅は 1/240\mathrm{s} (MPS法のときは 1/600\mathrm{s} )にしてあります。
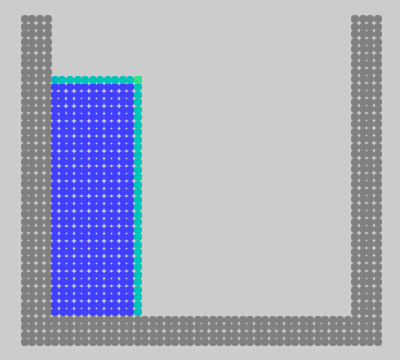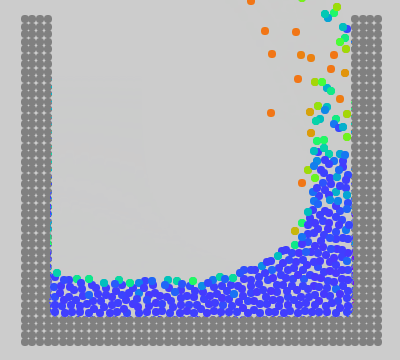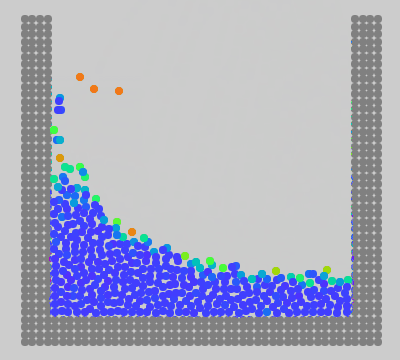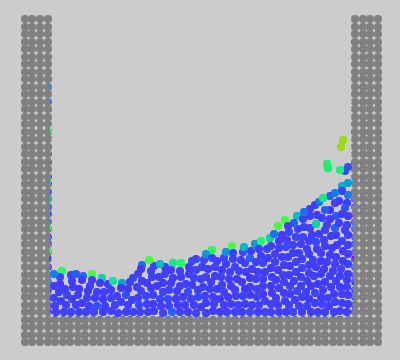
圧縮も爆発もせず、比較的大きな時間刻み幅で計算できています。
また、圧力の計算部分で速度に対する拘束条件を設定しているので、広く使われている剛体物理演算のソルバと組み合わせて圧力を解くことができます。ゲームでは流体・剛体の連成シミュレーションを行うことが非常に多いので、これは大きな利点になるのではないでしょうか。
以下、理論的な部分の解説です。
概要
離散化の手法はSPH法をベースにして、粘性の計算だけMPS法のものを用いています。また、粒子の移動を行う前に移動後の粒子数密度 n^* を線形近似し、それが一定密度 n^0 以下になるような拘束力として圧力 p を求めます。速度を拘束条件に用いるので VCSPH (Velocity-Constrained SPH) 法と勝手に名前を付けておきます。
重み関数
SPH法の W_{spiky} と同じ重み関数 W を使います。SPH法で使ったものと同じなので、正規化されています。
\begin{aligned}
W(r)&=a_1(r_e-|r|)^3\\
a_1&=\begin{dcases}
\frac{10}{\pi r_e^5}&(2D)\\
\frac{15}{\pi r_e^6}&(3D)
\end{dcases}\\
\nabla W(r)&=a_2(r_e-|r|)^2\frac{r}{|r|}\\
a_2&=\begin{dcases}
-\frac{30}{\pi r_e^5}&(2D)\\
-\frac{45}{\pi r_e^6}&(3D)
\end{dcases}
\end{aligned}
空間微分の離散化
VCSPH法における空間微分の離散化方法を定めます。まず、SPH法の離散化モデルに従い、物理量 \phi の勾配 \nabla\phi を定めます。
\begin{aligned}
\nabla\phi(x)=\sum_j\phi_j\Delta r\nabla W(x-x_j)
\end{aligned}
ここで \Delta r は1粒子あたりの体積(2次元の場合は面積)です。
次にラプラシアンですが、ラプラシアンをSPHのモデルで離散化するとカーネルの2階微分が生じ、 \nabla^2W(r) が r\rightarrow0 で発散してしまうため、数値的な不安定性の原因になる可能性があります。そこで、ラプラシアンに対してはSPH法ではなくMPS法のモデルを適用して、次のように定義します。
\begin{aligned}
\nabla^2\phi_i&=\frac{2d}{\lambda}\sum_j(\phi_j-\phi_i)\Delta rW(x_j-x_i)\\
\lambda&=\sum_j|x_j-x_i|^2\Delta rW(x_j-x_i)
\end{aligned}
d はシミュレーションの次元で、2次元なら 2 、3次元なら 3 です。
発散は今回使わないので定義しませんが、必要に応じて W を使って定義することができます。
圧力計算
VCSPH法では、MPS法と同様に粒子数密度 n を一定に保つように圧力を計算します。1ステップの計算は次のように行われます。
- 粘性項・外力項を計算し、粒子の仮の速度 v^* を求める
- 移動後の粒子数密度を n^0 に補正するような速度 v が得られる圧力 p を求める
- 圧力 p を用いて圧力項を計算し、次の時刻の真の速度 v と位置 x を求める
MPS法と異なる点は、粒子の仮の位置を求めない点と、速度を媒介変数として圧力を求める点です。粒子の仮の位置を求めないため近傍粒子探索のコストが低減されています。
2.と3.で使う式を導出しましょう。まず、粒子 i の粒子数密度 n_i を次のように定義します。
\begin{aligned}
n_i=\sum_j\Delta rW(x_i-x_j)
\end{aligned}
W が正規化されているので初期配置での粒子数密度は1になるはずですが、積分を総和で近似しているため多少のずれが生じます。そのためMPS法と同じように初期配置における粒子数密度を n^0 とし、この状態を非圧縮状態とします。
移動後の n_i の値を予測したいため、 n_i の時間微分を求めます。
\begin{aligned}
\frac{\partial n_i}{\partial t}&=\sum_j\frac{\partial}{\partial t}\Delta rW(x_i-x_j)\\
&=\sum_j\Delta r\frac{dW'}{dr}(|x_i-x_j|)\frac{\partial|x_i-x_j|}{\partial t}\\
&=\sum_j\Delta r\frac{dW'}{dr}(|x_i-x_j|)\left(\frac{x_i-x_j}{|x_i-x_j|}\cdot(v_i-v_j)\right)
\end{aligned}
W' は W の入力をMPS法のときのようにスカラーにしたもので、次を満たします。
\begin{aligned}
W(r)=W'(|r|)
\end{aligned}
これより、移動後の粒子数密度 n_i^* ※19MPS法のときは n^* が仮の粒子数密度になっていたため、混乱しないように気を付けてください。は現在の粒子数密度 n_i を用いて次のように表されます。
\begin{aligned}
n_i^*=n_i+\Delta t\sum_j\Delta r\frac{dW'}{dr}(|x_i-x_j|)\left(\frac{x_i-x_j}{|x_i-x_j|}\cdot(v_i-v_j)\right)
\end{aligned}
n が v の1次式になっていることに注目してください。
これが n^0 になるように真の速度 v の方を圧力 p を使って調整してやります。
次に、速度と圧力の関係を求めましょう。非対称性を修正したSPH法の勾配モデルに従って圧力項を計算します。
\begin{aligned}
-\nabla p_i=-\sum_j\frac{p_i+p_j}{2}\Delta r\nabla W(x_j-x_i)
\end{aligned}
これを仮の速度 v^* に適用して真の速度 v を得ます。
\begin{aligned}
v_i=v^*_i-\frac{\Delta t}{\rho_i}\sum_j\frac{p_i+p_j}{2}\Delta r\nabla W(x_j-x_i)
\end{aligned}
ここでも v が p の1次式になっていることに注目してください。
これで「粒子数密度と速度」と「速度と圧力」の1次の関係式が得られたので、両者をどうにかして繋げば「粒子数密度と圧力」の1次の関係式が得られるはずです。
……はずなのですが、実体に試してみると式がとんでもなく複雑になり、計算量が近傍粒子数の2乗オーダーで増えていく関係式が出来上がります。そこで考え方を変え、関係式を数値計算により求めることにします。関係式はどんなに複雑でも高々1次の式ですから、次のように書くことができます。
\begin{aligned}
n^*_i=A_ip_i+B_i
\end{aligned}
A_i と B_i は n^*_i と p_i によらない値が入ります※20ただし、 B_i の値は粒子の速度によって変化するので、反復法を回す途中で毎回計算する必要があります。。 A_i および B_i の値は、次のような手順で「計る」ことができます。
- すべての粒子の圧力を 0 と仮定したときの速度を使って n^*_i を求め、 n^{old}_i とする
- 粒子 i の圧力だけを p_i=1 と仮定したときの速度を使って n^*_i を求め、 n^{new}_i とする
- A_i=n^{new}_i-n^{old}_i,\ B_i=n^{old}_i
試しに圧力 p_i=1 を適用して n^* の変化を計れば係数が分かるという考え方です※21同様の手法は、剛体物理計算の分野において、拘束力に対する速度変化を求める際にも使われることがあります。単純ですが、かなり強力な手法です。。これらが分かれば、次の連立一次方程式を反復法で解くことができます。
\begin{aligned}
\forall i,\ n^*_i=n^0
\end{aligned}
これは見た目上は n^* に対する拘束条件ですが、 n^* が速度 v で表されるため、実質的には速度 v に対する拘束条件として解くことができます。
これで大体完成なのですが、SPH法やMPS法で問題となった負圧による不安定性の問題がまだ残っています。負圧は n^*_i<n^0 のときに周りの粒子を引き寄せようとして発生するため、不必要な場合に圧力が働かなくなるように条件式を次のように変更します。
\begin{aligned}
\forall i,\ p_i&\geq0,\\
n^0-n^*_i&\geq0,\\
(n^0-n^*_i)p_i&=0
\end{aligned}
これは線形相補性問題と呼ばれ、拘束力を求めるときによく出てくる式です※22剛体物理計算における拘束力の計算も、速度と拘束力に関する線形相補性問題を解くことで求まります。これらのソルバはほとんど同じような形をしているので、流体と剛体の連成シミュレーションを容易に行うことができます。。この方程式はProjected Gauss-Seldel法などを用いて解くことができます。
壁粒子
SPH法と同じように壁粒子を配置することで壁が再現できます。このとき、壁粒子が圧力によって受ける速度変化を0としてやることで、 A_i を壁粒子が動かないことを加味した上で計算ことができます。
動かしてみた
先に載せたとおりですが、解像度を上げた版は次のような結果になりました。

おわり
いい感じの手法が作れたので満足していますが、調べたら似たような手法がいくつか発見されました。それらについてはまた今度詳しく見てみることにしたいと思います。
* 明日のAdvent Calendarはphi16さんの記事です
注釈
| 1. | ↑ | 連続体は数式上では無限の細かさを持ちますが、コンピューターで計算できるのは有限の細かさです。無限の細かさを持つものを有限の細かさに落とし込むことを離散化と言います。 |
| 2. | ↑ | 物体が持つ物理的なパラメータのことを物理量と言います。例えば速度、温度、質量などは物理量です。 |
| 3. | ↑ | なんでこうするかは知りませんが、ほとんどの文献でこうなっています。詳しい理由を知っている方がいたら教えてください。 |
| 4. | ↑ | ちなみに、止まっている視点から見た速度変化のことを速度のオイラー微分と言いますが、今回は出番がありません。 |
| 5. | ↑ | 粘性係数 \mu を密度 \rho で割ったものです。 |
| 6. | ↑ | 時間 t ではなく、空間の座標軸 e_x,e_y,e_z に沿った偏微分を行う演算子のことです。 |
| 7. | ↑ | この式は「定数スカラー場 1 のラプラシアン」を意味します。 |
| 8. | ↑ | k の値を大きくするほど、安全に(爆発せずに)計算できるタイムステップ幅 \Delta t が小さくなります。安全に計算できるタイムステップ幅を評価する方法もありますが、ここでは割愛します。 |
| 9. | ↑ | 2次元だと積分範囲が円になり、3次元だと積分範囲が球になるためです。 |
| 10. | ↑ | こうなるともはや水ではないですが、元々水の粘性が小さいため、そこまで非現実的な値でもないはずです。 |
| 11. | ↑ | W_{poly6} カーネルは r=0 付近で値が一定になり、粒子の距離に対する値の変化が鈍くなります。このため圧力計算では W_{spiky} を使ったのですが、同じ問題が密度計算でも現れているのではないか、という推測です。 |
| 12. | ↑ | ただし、流体の十分内部にある粒子、具体的には影響半径内全体に粒子が均等に存在するような粒子に対して計算しておく必要があります。界面付近の粒子で計算すると値が小さくなってしまうためです。 |
| 13. | ↑ | これは、時刻 t+\Delta t における圧力を求めるのに時刻 t+\Delta t における圧力が必要であることを意味します。このような計算方法を「陰解法」( \leftrightarrow 陽解法)といいます。MPS法のSは “Semi-implicit” の頭文字であり、圧力計算のみに陰解法が使われることを意味しています。 |
| 14. | ↑ | 式中の (p_j-\hat p_i) が常に非負になるためです。 |
| 15. | ↑ | このように、直接解の値を定める境界条件のことをDirichlet境界条件といいます。 |
| 16. | ↑ | このように、解の境界に垂直な方向の勾配を定める境界条件のことをNeumann境界条件といいます。 |
| 17. | ↑ | 圧力勾配0のNeumann境界条件は、直感的には、方程式を解く際に粒子 i に隣接する壁の内部の粒子に、粒子 i の圧力をコピーすることで実現できます。しかし、これは壁の内部の粒子を方程式から除外することに等しくなります。 |
| 18. | ↑ | 局所的に2粒子しか存在しない場合、MPS法の勾配モデルではどう頑張っても圧力の勾配が0になります。 |
| 19. | ↑ | MPS法のときは n^* が仮の粒子数密度になっていたため、混乱しないように気を付けてください。 |
| 20. | ↑ | ただし、 B_i の値は粒子の速度によって変化するので、反復法を回す途中で毎回計算する必要があります。 |
| 21. | ↑ | 同様の手法は、剛体物理計算の分野において、拘束力に対する速度変化を求める際にも使われることがあります。単純ですが、かなり強力な手法です。 |
| 22. | ↑ | 剛体物理計算における拘束力の計算も、速度と拘束力に関する線形相補性問題を解くことで求まります。これらのソルバはほとんど同じような形をしているので、流体と剛体の連成シミュレーションを容易に行うことができます。 |
こんばんは.MPS法を専門として研究している大学院生です.
記事の内容,非常に興味深かったです.
MPS法は論文の形で共有されていない技術的知見が多々あり,そこで失敗するのは致し方ないことだと思います.
通常MPS法で解析を行う場合は,仮速度仮位置の計算後に,近づきすぎた粒子に対し非弾性衝突による斥力を加える処理を入れます.
|r_ij|<r_eを満たす粒子i, jにおいて,衝突処理後の速度をu**_i, u**_jとすると,
u**_i = u*_i + n_ij × (u*_ij・n_ij (e+1))/2
u**_j = u*_j – n_ij × (u*_ij・n_ij (e+1))/2
ここでu*_ij = u*_j – u*_i, n_ij = u*_ij/|u*_ij|, r_eは衝突処理を行う半径, eは衝突係数です.
r_eは初期粒子間距離の0.5倍,eは0.2ぐらいで設定するとうまく解析できると思います.
これらの処理は「粒子法」(越塚誠一著,丸善,2005)のサンプルソースにも含まれています(本文に記述はありません).
他に計算の安定化のために,圧力のポアソン方程式における係数行列の対角項に微圧縮性を許容する項を追加することが多いです.
∇^2 p^{k+1} = – ρ_0/Δt^2 {(n*-n^0)/n^0 – αp_i^{k+1}}
このαは音速を由来とする物理量ですが,実際には解析の挙動を見ながら丁度良いパラメータを選択する必要があります.
大体1.0e-6~1.0e-7ぐらいから始めて,圧縮が効きすぎる場合は1.0e-9~1.0e-12ぐらいまで小さくすると良いです.
こちらは詳細が上記の「粒子法」に書かれています.
よかったら参考にしてください.
こんばんは、非常に為になるコメントをいただきありがとうございます。
> 通常MPS法で解析を行う場合は,仮速度仮位置の計算後に,近づきすぎた粒子に対し非弾性衝突による斥力を加える処理を入れます.
> …
> これらの処理は「粒子法」(越塚誠一著,丸善,2005)のサンプルソースにも含まれています(本文に記述はありません).
こちらの本は私も持っていて実装の際にかなり参考にしたのですが、お恥ずかしながらサンプルソースをきちんと読んでいなかったため、衝突処理の部分を見落としていました。すり抜け防止ないしは近づきすぎ防止のために衝突処理を入れるのは非常に納得がいきます。
> 他に計算の安定化のために,圧力のポアソン方程式における係数行列の対角項に微圧縮性を許容する項を追加することが多いです.
こちらは本文で触れられていたため認識はしていたのですが、数値的安定性に効果があることを理解していませんでした。時間刻み幅Δtが小さくなるに従い圧力が非常に大きくなり、重力により粒子が落下する前に分散してしまう問題に悩まされていたのですが、Δtが小さくなるに従い圧縮の影響が相対的に大きくなるのでそのような現象が抑制されるのでしょうか。
どちらも時間のあるときに実装して、挙動が改善するか試してみようと思います。
ありがとうございました。
こんにちは。天文系の研究室でSPH法を研究している院生です。
天文分野以外でのSPH法の使われ方についてはほとんど知識が無かったため、大変興味深く読ませていただきました。
SPH法の離散化で微小体積をm/\rhoで与える理由ですが、元々SPH法がターゲットとしていた天文シミュレーションでSPH粒子の体積を定義することが困難だからだと思います。というのも、天文シミュレーションでは流体が音速を超える場合が頻繁にあり、衝撃波や膨張波などによって目まぐるしく流体の密度やSPH粒子同士の間隔が変化してしまうからです。また、密度を
\rho_i = \sum_j m_j W_ij
で計算できるというメリットもあります。連続の式の代わりにこの式を使うことで、膨張波によって粒子が少なく空間解像度が低下した領域でも密度が確実に正の値を取ることができます。
とはいえ、微小体積をm/\rhoとしなければならないという必然性は無く、任意の物理量Xを用いて
dr ~ X_i / \sum_j X_j W_ij
で体積を与えることができます。近年天文業界ではこの手法が注目されていて、Xとして圧力や内部エネルギー、エントロピーなどを用いるスキームがよく計算に使用されています。
こんにちは、コメントいただきありがとうございます。
私は粒子法を専門に研究しているわけではないので恐縮ですが、CG分野での利用に少しでも興味を持っていただけたならば幸いです。
微小体積をm/ρで与えるのにそのような背景があったのですね。確かに大きな圧縮や膨張が生じる場合では粒子ごとの体積を直接定義するのは不適当なように思えます。
>とはいえ、微小体積をm/\rhoとしなければならないという必然性は無く、任意の物理量Xを用いて
>dr ~ X_i / \sum_j X_j W_ij
>で体積を与えることができます。…
密度以外の物理量を使って微小体積を与える手法は全く知りませんでした。このような手法も研究されているんですね。
大変勉強になりました。ありがとうございます。
内容を拝見して興味を持ったのでコメントです。
SPHの内容についてですが、Muller(2003)”Particle-based fluid simulation for interactive applications”の内容を用いた離散化方法だと思います。この方法はCG向けにリアルタイム計算ができるように定式化されたものなので、物理的な計算になっていない部分が多くあります(重み関数を演算子ごとに変更したり・・・)。離散化手法で、圧力項や粘性項に不自然な変換があったのもそのためです。
つまり、物理的な計算を真面目に行おうとした場合はSPHは一般的にこのような離散化の式は(私の知る限り)使わず、完全にCGのみで使われる離散化手法です。ちなみに、一般的なSPHでは物理法則のみから力の非対称性が起こらないような定式化がされています。MPSやSPHで真面目な計算を目指す場合は、後藤仁志さんの「粒子法:連続体・混相流・粒状体のための計算科学」という本を読むことをお勧めします。この本に全部書いているわけではありませんが、最近の技術を使えば人工的な衝突による力や圧縮率などなくても安定した計算が高精度にできるようになっています。興味があれば本の内容をもとに最近の論文など見てみると面白いかもしれません。また、CG向けだとPosition Based Fluidsという技術が最近人気になっています。非圧縮流体のリアルタイム計算を3次元で行いたいならPosition Based Fluidsの情報を調べてみることをお勧めします。ただ、CG版SPHよりもさらに式が物理的ではなくなります。また、機械学習に関しても記事があるようなので伝えておくと、粒子法の計算をもとに機械学習を使った計算方法も最近は頻繁に提案されています。
密度の単位についてですが、(計算する次元に関係なく)1000kg/m^3だと思います。体積(m^3)を質量(kg)/密度(kg/m^3)にするのは、この次元からも分かるように物理の式で質量(kg)=体積(m^3)×密度(kg/m^3)というのがあるからです(正確には体積積分ですが)。2次元の場合は、例えば奥行き方向は単位長さで考えているとしてやるとわかりやすいかもです。つまり、粒子間距離をlとすると2次元では体積は1×l^2ですし3次元ではl^3です(計算領域を等間隔にlの長さの4角形の領域で分けたと思えばわかりやすいかもです)。この情報から各粒子の質量は水の場合、質量(kg)=1×l^2(m^3)×1000(kg/m^3)と計算できますね。
今後も頑張ってください。応援しています。
非常に詳しいコメントありがとうございます。
CG目的でないSPHでは離散化の式が違うというのは知りませんでした。
> MPSやSPHで真面目な計算を目指す場合は、後藤仁志さんの「粒子法:連続体・混相流・粒状体のための計算科学」という本を読むことをお勧めします。
実はこの本は発売当初から気になっていたので、今度購入してみようと思います。Position Based Fluidsや機械学習を用いた方法についても調べてみます。
> ただ、CG版SPHよりもさらに式が物理的ではなくなります。
やはりそうなりますよね……。機械学習などでは特に「どううまく見せるか」が焦点になっていることと思います。
密度と質量に関しても分かりやすい説明をありがとうございます。
これからも粒子法に触れる機会は多いと思うので頑張ります。
最新の境界潤滑理論、CCSCモデルを粒子法でモデル化したら面白いかもしれませんね。
EHL理論の専門家であれば、油膜は絶対に切れないというでしょうね。しかし境界潤滑状態というのもうすでに油膜は切れています。電気抵抗を計った実験が調べればたくさん出てきます。しかし問題は「油膜が切れる」と言いたくなるような突然死(サドンデス)が起こるのはなぜかということです。それに明確な答えを出したのが久保田博士のCCSCモデル。なんと潤滑油由来の表面に張り付いたグラファイト膜(トライボフィルム)がナノメートルのダイヤモンドになるというものです。詳しくは「境界潤滑現象の本性」で検索してみてください。文献をさかのぼるとC.C.Yangらの文献にはコールドスタートでエンジンが痛む理由も分かります。