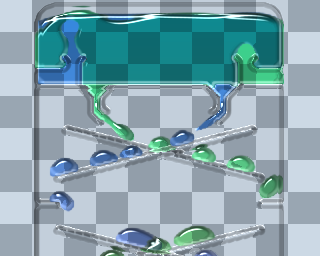
Flash+Stage3Dでオイル時計のシミュレーションを作ってみました。
流体は全てGPGPUで計算しています。
ドラッグで流体を混ぜられます。
スペースキーを押すと上下をひっくり返します。
>> Open simulation (Required Flash Player 18 or later)
>> View source code
以下は主に流体のシミュレーション方法についての解説です。
基本的な部分は前回のStable Fluidsと似ているので、そちらを先に理解して
おくことをお勧めします。
今回の方がもう少し厳密なシミュレーションになっています。
Stable Fluidsとの違いは
- 2種類の流体を計算する(混相流)
- 流体の密度が一定でない
- 界面に表面張力が発生する
などです。
準備
まずは流体を表現する格子について。
前回同様、テクスチャを格子に見立てて計算を進めていくわけですが、今回は
スタッガード格子というものを使いました。
普通の格子では、格子の中央部分に全ての情報を定義しますが、スタッガード格子では
情報の種類に応じて格子のどの位置に定義するかを変えます。
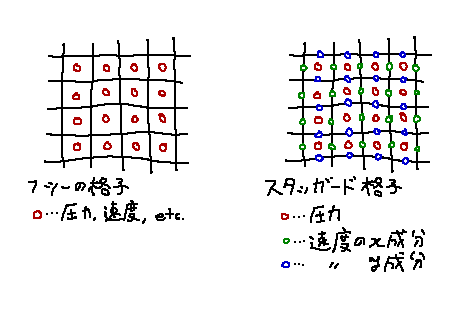
格子モデルの違い
一見複雑で面倒そうなスタッガード格子ですが、実はこれを使うと後の計算が
かなり楽になってくれます。
次は流体の表現方法について。
前回は全ての領域が一様な流体で満たされていましたが、今回は2種類の流体を
計算するのでそういう訳にもいきません。
そこで、各流体が格子(セル)にどれだけ存在するかを0~1で表した数値(VOF値)
を使って計算を進めます。(Volume of fluid methodも参照)
あるセルについて、2つの流体 f , g のVOF値をそれぞれ V_f , V_g とすると、
それらは次の条件を満たすべきです。
また、2つの流体の密度(1セル当たりの質量)を \rho_f , \rho_g とすると、セルの質量は
VOF値を使って次のように表せます。
重力の適用
先程の2種類のVOF値を使って、スタッガード格子に定義された速度に重力を加えます。
今回は流体 f だけに重力 \vec{g} = (g_x, g_y) を加えるとします。
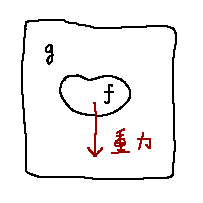
流体fだけに重力を加える
さて、全てのセルには図のように対応するx方向、y方向の速度が定義されています
(ただし隣り合うセルと速度を共有していることに注意)。
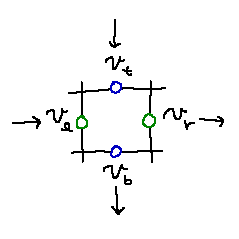
矢印は速度の正の向き
流体 f に重力を加えるには、速度を次のように更新します。
\begin{aligned} v_l \leftarrow v_l + \frac{1}{2}V_fg_x\\ v_r \leftarrow v_r + \frac{1}{2}V_fg_x\\ v_t \leftarrow v_t + \frac{1}{2}V_fg_y\\ v_b \leftarrow v_b + \frac{1}{2}V_fg_y \end{aligned}速度の定義点が、VOF値の定義点であるセルの中央から半分ずれているため、
上下左右の速度に半分ずつ重力を加えてやる必要があります。
速度の発散
スタッガード格子を使うことで発散の計算が直感的で簡単になります。
あるセルの速度の発散は次で計算できます。速度の正の向きに注意してください。
圧力による速度場の補正
前回の解説にもあったように、流体の速度場の発散は0である必要があります。
そのために必要な圧力を計算することになりますが……その前に、圧力によって
どれだけ速度が変化するかを求めます。
各セルの中央に定義された圧力 p が求まったとします。この圧力を
速度場に適用したときに、速度がどう変化するかを考えます。
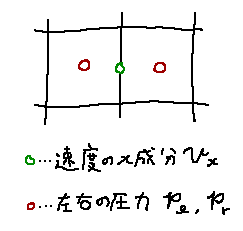
2つのセルに挟まれるx方向の速度
簡単にするため、図のようにx方向の速度に限定して考えます。
圧力とは、単純に言えばそのセルが周りのセルを押し返す力なので、左右のセルの
境界部分は左から p_l 、右から p_r の力で押し返されます。
x方向の速度は右向きが正であることに注意すると、左右のセルの境界部分が受ける力は
p_l - p_r であることが分かります。
では v_x に p_l - p_r を加えたいところですが、忘れてはならないものがあります。
セルの質量です。
今回のシミュレーションでは流体の密度が一様ではないため、セル毎の質量の違いを
考慮してやる必要があります。
左側の質量を m_l 、右側の質量を m_r とします。速度の定義点は左右のセルの
中央にあるため、二つのセルの平均をとって質量 \frac{m_l + m_r}{2} のセルの中央にあるとみなします。
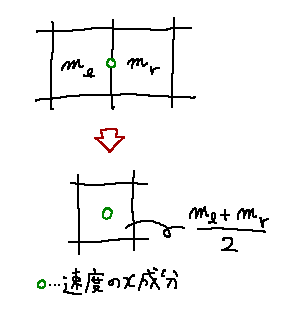
そして速度に圧力差 p_l - p_r を質量 \frac{m_l + m_r}{2} で割った値を加えます。
すなわち、速度の更新は次のようになります。
y方向に関しても同様に更新します。
\begin{aligned} v_y \leftarrow v_y + (p_t - p_b)\frac{2}{m_t + m_b} \end{aligned}
圧力を求める
さて、圧力によってどのように速度場が変化するかが分かったところで、いよいよ圧力を
計算します。
あるセルの圧力は、隣接するセルと共有する速度すべてに影響を与えるため、圧力の
満たすべき式は巨大な連立1次方程式になります。
これをそのまま解くのは現実的ではないので、前回同様に反復法を使って解きます。
反復法を利用して圧力を求めるのに必要な式は、
「他の全てのセルの圧力が求まったときに、自分のセルの圧力を求める式」
だけです。これなら求まりそうな気がしますね。
それでは圧力が満たすべき式を追っていきます。最終的な目標は全てのセルにおいて
速度の発散
が0となることでした。より正確には、圧力適用後の速度の発散が0になればいいので、
圧力適用後の左右上下の速度 v_l' , v_r' , v_t' , v_b' を
として、
\begin{aligned} \mathrm{div}\vec{v'} = v_r' - v_l' + v_b' - v_t' = 0 \end{aligned}が満たすべき式です。ここで、
p_l , p_r , p_t , p_b はそれぞれ左右上下に隣接するセルの圧力、
m_l , m_r , m_t , m_b はそれぞれ左右上下に隣接するセルの質量です。
これを p について解くと、最終的に次の式が得られます。
\begin{aligned} p = \frac{(w_lp_l + w_rp_r + w_tp_t + w_bp_b) - (v_r - v_l + v_b - v_t)}{w_l + w_r + w_t + w_b} \end{aligned}ここで、
\begin{aligned} w_l = \frac{2}{m_l + m}\\ w_r = \frac{2}{m_r + m}\\ w_t = \frac{2}{m_t + m}\\ w_b = \frac{2}{m_b + m} \end{aligned}です。
この方程式は、次のように反復法で解くことができます。
- 圧力 p の配列を適当な値で初期化する
- 配列の各要素の値を先程の式に従い更新する
- 収束するまで(あるいは予め決められた回数だけ)2を繰り返す
2をどのように処理するかによって、反復法がヤコビ法になったりGauss-Seidel法になったり
SOR法になったりチェッカーボードSOR法になったりします。
詳しくはググってください。ちなみに今回はチェッカーボードSOR法を採用しました。
余談ですが、この p に関する方程式は、次の方程式を離散化(有限の情報での計算に
置き換えること)したもので、このような形の方程式はポアソン方程式と呼ばれています。
表面張力の計算
丸い油滴を作るためには表面張力が不可欠です。表面張力は流体が自身を引き合うことで
生じる力なので、引力を発生させることで再現できます。
引力の和として、表面(界面)付近の流体に「内部へ押し込む力」を加えてやります。
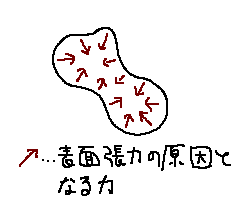
体積を減らそうとする力が表面張力を生み出す
この引力自体は表面張力ではありませんが、圧力(正確には圧力の勾配)と
合わさることで表面張力としての作用が生まれます。
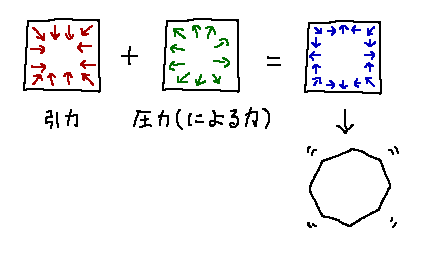
圧力と重なり表面積を減らそうとする力に
では引力の計算方法ですが、これは高さマップからの法線マップの作成
と同じ要領で計算できます。VOF値を適当にぼかしたテクスチャを作り、上下左右との
差分を取るだけです。

計算された「引力」マップ
この引力を流体 f , g についてそれぞれ計算し、それらをVOF値で混ぜ合わせて
速度場に加えます。
すなわち、2つの流体の引力を \vec{s_f} , \vec{s_g} として、次のように速度場を更新します。
αは適当な係数です。何度も値を変えていい感じの動きになるまで調節します……
実際にプログラムにするときは、速度場がスタッガード格子で定義されていたことに
注意してください。重力と同じように、セルの上下左右の速度に分配してやる必要があります。
移流計算
流れを作るためには、速度場に従ってVOF値と速度場自身を移流させる必要があります。
速度場の移流は、スタッガード格子を使っていることを除いて前回と同じ方法ですので
詳細は割愛します(セミラグランジュ法というらしいです)。
さて、速度場の方は割と適当に移流させても(少なくとも見た目上は)問題ないのですが、
VOF値の方は適当に移流させると困ったことが生じます。VOF値の総量が保存しない
のです。いつの間にか減ってたり増えてたりします。
最初の方に出てきたVOF値が満たすべき式を思い出してください。
\begin{aligned} V_f + V_g = 1 \end{aligned}初期状態からVOF値の総量が変化してしまうと、この式を満たせなくなります。
どこかのセルで流体が足りなくなったり、溢れ出したりしてしまいます。
ですのでVOF値に関しては総量が保存するように移流させてやる必要があるのです。
ではどうするかというと、実は単純で、あるセルのVOF値を速度に沿って移動させた先の
セルに分配するだけです。
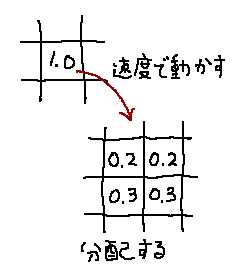
当然ながら分配の仕方には注意してやる必要があります。
移流前のセルの中央の座標に速度を加えたものを移流後の座標とし、その座標に
最も近い4つのセルにxy座標の差の比率でVOF値を分配します。
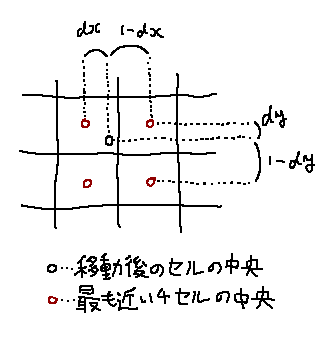
図のような比率になった場合、左上、右上、左下、右下のセルにそれぞれ
(1-dx)(1-dy):dx(1-dy):(1-dx)dy:dxdy
の比率でVOF値を分配します。バイリニア補間と同じです。
これを全てのセルに対して計算すれば移流計算は完了です。
…と言いたいところですが、このままではまともにシミュレーションが動きません。
何故かというと、VOF値がぼけてしまうからです。実際に動かしてみたのが次です。

VOF値に対する数値粘性が発生し、界面がぼけてしまう
青色が流体 f 、赤色が流体 g のVOF値です。見ての通り、シミュレーションが
進むにつれて2つの流体のVOF値が混ざってしまっています。
これではそもそも界面がどこか分からないので表面張力もあったものではありません。
そこで、表面張力の計算方法を変更します。今までは
- VOF値から表面張力(を発生させる力)を計算する
- 表面張力とVOF値を見て速度場を更新する
- 速度場を見てVOF値を移流させる
でしたが、これを次のように変更します。
- VOF値から表面張力(を発生させる力)を計算する
- 速度場と表面張力を見てVOF値を移流させる
- 表面張力とVOF値を見て速度場を更新する
2が重要です。2つの流体の表面張力を混ぜ合わせた力ではなく、それぞれの流体に
個別に表面張力を作用させます。
この処理により、同じセルにあるVOF値でも、流体の種類によって別の方向に
移流することができるようになります。
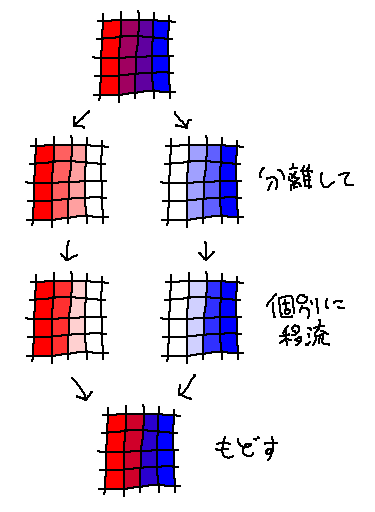
界面が圧縮する
この処理を加えた後のシミュレーションが次です。VOF値が全くぼけなくなっています。

VOF値の補正
以上で流体のメインとなる計算部分は全て完了しました。……が、まだ解かなくては
ならない方程式が一つ残っています。
それは、VOF値の満たすべき式
\begin{aligned} 0 \leq V_f \leq 1\\ 0 \leq V_g \leq 1\\ V_f + V_g = 1 \end{aligned}です。
今までの計算が誤差無しで完璧に行われればこの処理は不要ですが、実際のところ
かなりの誤差が残ってしまいます。とりわけ引力を加えたことにより界面付近で
となってしまうセルが多数発生します。これを修正しなければなりません。
ではどう修正するかですが、これには隣り合うセルとVOF値の受け渡しを行う
ことが考えられます。
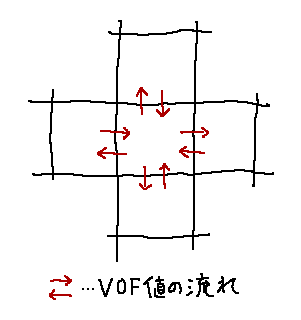
隣接するセルにVOF値の流れを作る
この受け渡しの量を調整して、全てのセルで V_f + V_g = 1 が満たされるように
してやればOKです。
しかし、このままでは受け渡しの方法が一意に定まりません。自由度が高すぎるためです。
少し考えてみると、受け渡し量を設定することによってVOF値の配分を「任意に」変えられる
ことが分かるかと思います。
そこで、受け渡し量に関して次の制約を加えます。
まず、受け渡し量は、 V_f と V_g の合計値についてのみ考えることに
します。つまり、セルの境界1辺につき符号付きの受け渡し量を1つだけ定義します。
次に、受け渡し量は、各セルの中央に定義される別の変数 p_V によって決定される
ものとします。この変数は「受け渡し量に関する圧力」のようなものです。この「圧力」が
高いセルから低いセルへVOF値の合計が流れるように受け渡し量を設定します。
二つ目の制約が重要です。この制約によって、受け渡し量を p_V を求めることによって
決定でき、さらにこの p_V は p と同じ形の方程式で求めることができます!
実際に p_V を求める方程式を導きます。まず、隣接するセルとVOF値の受け渡し量を
左右上下のセルとの境界について、それぞれ flow_l , flow_r , flow_t , flow_b
とします。正の向きは速度の正の向きと同じにし、受け渡し量と p_V の関係は
次のように定めます。
ここで、 {p_V}_l , {p_V}_r , {p_V}_t , {p_V}_b はそれぞれ左右上下に隣接するセルの
p_V の値です。
また、セルの2つの流体のVOF値の合計値を V = V_f + V_g とします。
このとき、受け渡し後の V の値 V' は次のようになります。
最後に、 V' の満たすべき式 V' = 1 と合わせて p_V について式を解きます。
すると……
p に関する方程式とほとんど同じ形になりました。これを p と同じように反復法で
解くことで受け渡し量を求めることができます。
さて、受け渡し量は V_f と V_g の合計に関するものでした。
よって、 V_f と V_g を実際にどれだけの比率で受け渡しするかは、また別に
決めなければなりません。
今回は受け渡しを行うセルのうち、VOF値を渡す側のセルの V_f と V_g の比を使いました。
図の左側のセルが渡す側のセル、右側のセルが受け取る側のセルです。
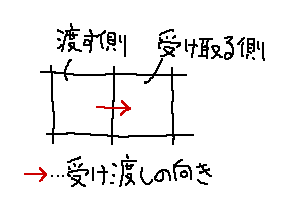
しかしこれではまだ問題点があります。
受け渡しを行った結果、VOF値が負になってしまうことがあるのです。
1以上の値ならまだしも、VOF値が負の値になってしまうとセルの質量も
ゼロ以下になりかねません。これを防ぐためには、受け渡しの際、セルから
流出するVOF値の量を制限する必要があります。
例えば、あるセルの V_f が0.5だった場合、そのセルから流出する(渡す)
V_f の値は流入(受け取る)量に関係なく0.5を超えないようにします。
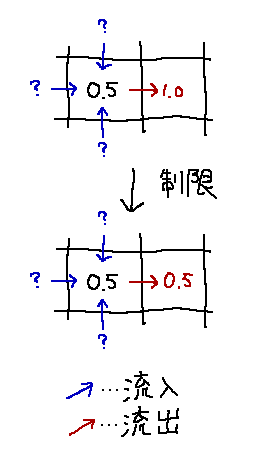
元々のVOF値を超えて流出しないよう制限する
この制限を行った後、実際にVOF値の受け渡しを行うことでVOF値の補正が完了します。
シミュレーションの進行とレンダリング
以上で流体シミュレーションの準備は完了です。お疲れ様でした。
後はこれらを正しい順番で計算するだけです。
フレーム内では、次のように計算を進めます。
- セルの質量の計算
- 重力やその他の外力の適用
- 速度の発散計算
- 圧力の計算
- 圧力の速度場への適用
- 表面張力(引力)の計算
- VOF値の移流
- 表面張力の速度場への適用
- 速度場の移流
- セルの質量の再計算
- VOF値の補正
- レンダリング
流体のレンダリングですが、VOF値が計算できてしまえばそのデータを使って
どうにでもできてしまいますので、あまり詳しくは書きません。
3方向くらいからの平衡光源でPhongの反射モデル+リムライティングをしてやると
それなりに液体っぽく見えてくれました。
屈折は法線ベクトルと逆方向にUV座標をずらすやり方で誤魔化してます。
もう少しかっこよくしたい感はありましたが、流体の計算自体がかなり重いので、
表示に凝り始めるとFPSが落ちてしまう心配もあるため適当に……
ちなみにVOF値の元データはこんな感じになってます。レンダリングだけで
見栄えが相当変わりますね。
オイル時計の向こう半分
実装に使った小技など
・ 表面張力を2種類に分けて適用した
解説では1種類しか書いてありませんが、実際には2種類の表面張力を使っています。
一つは解説にある通りで、もう一つが移流計算のみに用いる補正用です。
補正用の力はVOF値のぼかし方を小さくして作成します。こうすることで小さな
液滴も安定して作れるようになります。
・ 速度の最大値・最小値マップを事前生成した
移流計算の際、座標に速度を足した結果、壁の中に埋まってしまうことがないように
前もって各セルから安全に(壁に埋まらずに)移動できる量を計算しておきます。
座標に加える速度を、計算しておいたマップを参照して制限することで、
流体が壁に埋まる現象を回避できます。
・ 移流以外の計算には正規化されたVOF値を使った
セルの質量の計算や、表面張力の計算には V_f や V_g の値そのままではなく、
和が1になるように修正された値
を使っています。こうすることで、どうしても発生してしまうVOF値の誤差によって
シミュレーションが不安定になるのを抑えることができます。
最後に
今回は格子モデルでの流体計算に本気で挑戦してみましたが、やはり
粒子法と同様パラメータ調整が非常に大変であることが分かりました。
シェーダには自前のシェーダ言語のOGSLを使用しました。これがなかったら
全部アセンブリで書かないといけなかったのでまず完成しなかったことでしょう。
10か月前の自分に感謝。