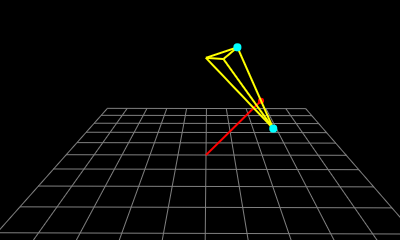
3次元空間内の単体(線分、三角形、四面体)と原点の最接近点を求めるコードを書きました。
以下アルゴリズムに関する解説とメモですが、長いので2回に分けて解説します(その2はこちら)。今回は点、線分、三角形の場合です(下のデモは四面体ですが……w)。
>> Run Demo (HTML5+JS)
なぜ書いたか
開発中のOimoPhysicsで使おうとしている GJK Algorithm という衝突判定のアルゴリズムがあります。一度実装してしまえば任意の凸形状に関して衝突判定ができるという凄いアルゴリズムなのですが、なかなか実装が大変です。GJKに関してはまた個別に記事を書く予定(多分)ですが、GJKを実装するためには「単体と原点の最接近点」を求めるコードを書く必要があります。
単体とは、平たく言うと「n + 1頂点からなる n 次元の図形」で、点、線分、三角形、四面体などがこれにあたります。これらと原点を結ぶ最も短い線分を求める必要があります。点はまあ良いとして、三角形、四面体となるとこれだけで結構大変です。
点と原点の最接近点
これはいいでしょう。点がそのまま最接近点になります。

線分と原点の最接近点
いよいよ本番です。始点 v_1 と終点 v_2 が与えられたときに、線分 v_1 v_2 と原点との最接近点を求めます。
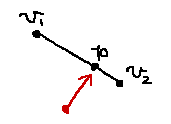
話を簡単にするために、一旦線分ではなく直線と原点との最接近点を求めます。直線 v_1 v_2 上の点は、パラメータ t を使って v_1+t(v_2-v_1) と表すことができます。つまり、この t をぐりぐりと動かしてやって、原点との距離(=長さ)が最小になるものを探せばOKということになります。
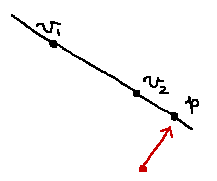
ここで、証明は省きますが、「ある点から直線上の最接近点へのベクトルは、直線と垂直になる」という性質を使います。すると p が最接近点の位置ベクトルのとき、 (v_2-v_1)\cdot p=0 が成り立ちます。 p は直線上の点だったので、さっきのパラメータを使った式を代入してやることで
(v_2-v_1)\cdot(v_1+t(v_2-v_1))=0が得られます。これを t について解くと、
\begin{aligned} t=-\dfrac{v_1\cdot(v_2-v_1)}{|v_2-v_1|^2} \end{aligned}となります。これで直線と原点の最接近点が求まりました。
ですが、欲しかったのは直線ではなく線分と原点との最接近点でした。続いて線分に対する方法を考えます。
実は、先程の式をわずかに変更するだけで線分と原点の最接近点を求めることができます。得られた t に対して、 t を 0 から 1 の間に収まるようにクランプするだけです。 t<0 の場合は最接近点が線分から v_1 方向に、 t>1 の場合は v_2 方向にはみ出しているためです。
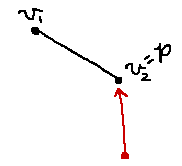
今回の 直線 → 線分 のように、「無限の大きさで考えてから、有限の大きさに落とし込む」方法は衝突判定においてかなり有用なので、覚えておくと得です。
三角形と原点の最接近点
いよいよ三角形です。これも線分と同じように、三角形上の点をパラメータで表してクランプすることで求まる……と嬉しいのですが、残念ながら上手く行きません(これで一回ハマりました)。
上手く行かない理由は下の図を見てもらえればなんとなく分かるんじゃないかなーと思います。主な原因は v_2-v_1 と v_3-v_1 が直交していないためですね。歪んだ空間上の最接近点が求まってしまいます。
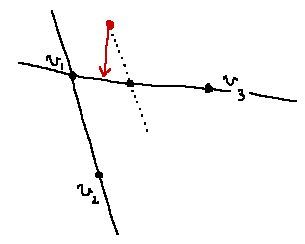
内積とかを使って無理やりやればもしかしたら求まるかもしれませんが、この後に四面体が控えているためできるだけシンプルな方法で求めたいと思います。
やや複雑な図形に対する判定では、場合分けを行うのがセオリーです。三角形と原点の最接近点を求める場合、どのような場合分けが発生するのか考えてみましょう。求まる最接近点の位置で場合分けを行うのが良さそうです。
ケース1: 三角形の面上に最接近点が存在するケース
こんな場合ですね。
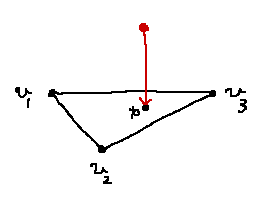
空間が3次元なのを忘れてはいけません。三角形の存在する平面上に下した垂線の足が三角形内に存在する場合にこうなります。
ケース2: 三角形の辺上に最接近点が存在するケース
こんな場合です。
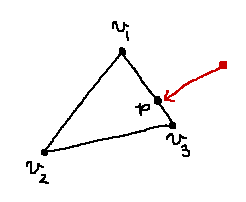
原点が辺から見て三角形の外側に存在する場合に発生しそうです。
ケース3: 三角形の点上に最接近点が存在するケース
最後はこんな場合です。
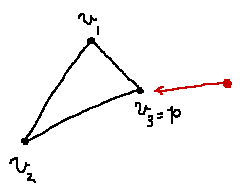
これも原点が辺から見て三角形の外側に存在する場合に発生しそうですが、その中でもどれかの頂点に最も近い場合です。
実際に場合分けする
以上3ケースについて場合分けしてみましたが、辺は3つ、頂点も3つあるので、実際にプログラムにする場合、ループを回すにしてもやや面倒な実装になります。そこで、ケース2とケース3を統合して「三角形の面内に最接近点がある場合」と「三角形の辺上(頂点含む)に最接近点がある場合」で場合分けを行います。また、三角形の辺は線分なので、線分と原点の最接近点を求めるコードを使い回すことができます。これで実装が楽になります。
では実際にどうやって判定するかですが…… 三角形を「3枚の平面で仕切られた内部」という風に捉えます。
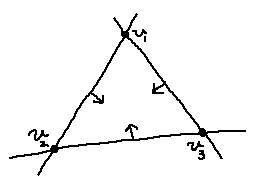
この向きのある平面3つに対してそれぞれ内外判定を行い、1つでも平面の外側にあれば三角形の辺上に、全ての平面の内側にあれば三角形の面上に最接近点があります。
ここで、原点が内側にあるような平面に対応する三角形の辺上には最接近点が存在しないことに気を付けてください。例えば下の図では、原点は平面 v_1v_3 と v_2v_3 の内側にありますから、最接近点が存在するとすれば辺 v_1v_2 上、または三角形の内部しかありえません。
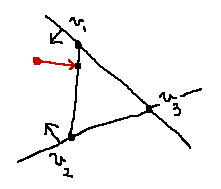
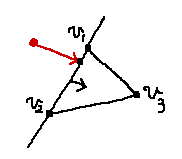
さらに言えば、原点がある平面の外側にあった場合、最接近点は必ずその平面に対応する辺上に存在します。つまり、原点が外側に存在するような平面を見つけた場合、直ちに三角形に対する判定を打ち切って線分と点に対する問題に帰着させることが可能になります。例えば下の図では、原点は平面 v_1v_2 の外側にありますから、最接近点は必ず辺 v_1v_2 上に存在します。
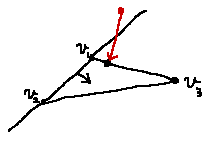
追記:これ後から気付いたんですが、何か動作がおかしいと思ったら下図のように鈍角三角形の場合は成り立ちませんでした。素直に3辺調べるしかなさそうです。残念……。
ある点 p に対する平面の内外判定は、平面上に存在する1点 v と、平面の外側を向いた法線ベクトル n が分かれば簡単に判定できます。 (p-v)\cdot n>0 なら点は平面の外側、 (p-v)\cdot n<0 なら内側です。
では最後に平面の外側を向いた法線ベクトルの求め方です。これは外積を使うことで案外あっさりと求まってしまいます。まずは三角形の法線ベクトルを求めます。三角形には裏と表がありますが、ここでは右手系を採用して「頂点が反時計回りに並んで見える面」を表面(=法線ベクトルが飛び出す方向)とします。このとき三角形の法線ベクトル n_{123} は
\begin{aligned} n_{123}=(v_2-v_1)\times(v_3-v_1) \end{aligned}で求まります。後はこの n_{123} を使うことで、それぞれの辺に対応する法線ベクトル n_{12},n_{23},n_{31} が次のように求まります。
\begin{aligned} n_{12}=(v_2-v_1)\times n_{123}\\ n_{23}=(v_3-v_2)\times n_{123}\\ n_{31}=(v_1-v_3)\times n_{123}\\ \end{aligned}まとめ
さて、長くなってしまいましたが、以上の内容をまとめると以下のようにして三角形と原点の最接近点を求めることができます。
まず三角形の法線ベクトル
\begin{aligned} n_{123}=(v_2-v_1)\times(v_3-v_1) \end{aligned}を求め、次に各辺に対応する法線ベクトル
\begin{aligned} n_{12}=(v_2-v_1)\times n_{123}\\ n_{23}=(v_3-v_2)\times n_{123}\\ n_{31}=(v_1-v_3)\times n_{123}\\ \end{aligned}を求める。続いて原点と各辺に対応する平面の内外判定を行う。
\begin{aligned} outer_{12}=-v_1\cdot n_{12}>0\\ outer_{23}=-v_2\cdot n_{23}>0\\ outer_{31}=-v_3\cdot n_{31}>0\\ \end{aligned}一つでも原点が外側にある平面が存在すれば、対応する辺(=線分)と原点との問題に帰着させる。
原点が外側にある平面に対し、対応する辺と原点の最接近点を求め、最も原点に近かったものを最接近点とする。いずれの辺に対しても内側に存在すれば、最接近点 p は三角形上に存在し、次のように原点を三角形の存在する平面上に射影することで求められる。
おわりに
三角形まででずいぶん長くなってしまいましたが、四面体の場合はまた場合分けで三角形の問題に帰着させることができます。すると今回のアルゴリズムを使い回すことができ、結果として実装は非常に楽になります。
四面体の場合の詳しい解説は次回です。