3次元空間内の単体(線分、三角形、四面体)と原点の最接近点を求めるコードを書きました。
前回は三角形までやりましたが、それの続きです。今回はあっさり終わります。
ヘッダ画像とデモは前回の使い回しです。
>> Run Demo (HTML5+JS)
前回までで三角形と原点の最接近点を求める方法が分かりました。
疑似コードを書いておくとこんな感じになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
// 線分と原点の最接近点を返す Vec3 getClosestPointOnLine(Vec3 v1, Vec3 v2) { // (略) } // 三角形の法線ベクトルを返す Vec3 getTriangleNormal(Vec3 v1, Vec3 v2, Vec3 v3) { return cross(v2 - v1, v3 - v1); } // 三角形と原点の最接近点を返す Vec3 getClosestPointOnTriangle(Vec3 v1, Vec3 v2, Vec3 v3) { Vec3 n = getTriangleNormal(v1, v2, v3); Vec3 n12 = cross(v2 - v1, n); Vec3 n23 = cross(v3 - v2, n); Vec3 n31 = cross(v1 - v3, n); boolean outer12 = dot(-v1, n12) > 0; boolean outer23 = dot(-v2, n23) > 0; boolean outer31 = dot(-v3, n31) > 0; Vec3 on12 = v1; Vec3 on23 = v1; Vec3 on31 = v1; if (outer12) { // 辺12上 on12 = getClosestPointOnLine(v1, v2); } if (outer23) { // 辺23上 on23 = getClosestPointOnLine(v2, v3); } if (outer31) { // 辺31上 on31 = getClosestPointOnLine(v3, v1); } if (outer12 || outer23 || outer31) { // 辺上 return min(on12, on23, on31); } else { // 三角形上 return dot(v1, n) / dot(n, n) * n; } } |
これに四面体と原点との最接近点を返す関数を追加します。方法は比較的シンプルで、三角形のときの手法の拡張です。
三角形の場合は次のように考えました:
・各辺の法線ベクトルを求める
・各辺と原点の内外判定を行い、
・原点が外側にある辺があれば、辺と原点の最接近点を求める
・求めた全ての点で最も原点に近いものを返す
・全ての辺に対して原点が内側にあれば、原点を三角形上に射影した点を返す
四面体では次のように考えます:
・各面(=三角形)の法線ベクトルを求める
・各面と原点の内外判定を行い、
・原点が外側にある面があれば、三角形と原点の最接近点を求める
・求めた全ての点で最も原点に近いものを返す
・全ての面に対して原点が内側にあれば、原点は四面体内部にあるので、原点を返す
見ての通り、三角形の場合とほぼ同じですが、四面体の場合は、点の配置によっては「表裏がひっくり返る」ことがあるので注意する必要があります。何のこっちゃ?と思うかもしれませんが、下の二つの四面体を見てください。
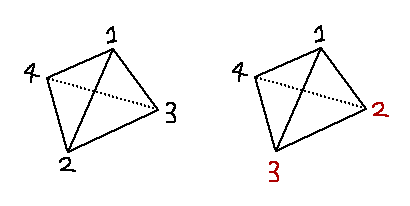
左の四面体で、外側から見て反時計回りに三角形の頂点を見ていくと、
・1→2→3
・1→3→4
・1→4→2
・2→4→3
の4つがあります。
一方、右の四面体はというと、
・1→3→2
・1→4→3
・1→2→4
・2→3→4
と、全ての面が逆向きになっていることが分かります。この違いを考慮しないと、面に対する原点の内外判定がおかしなことになってしまいます。
ではどうやって四面体が反転しているのを検出するか、というのが問題になりますが、これはベクトルの外積を使うと簡単にできます。三角形 v_1, v_2, v_3 の法線ベクトル (v_2-v_1)\times(v_3-v_1) は、常に「 v_1, v_2, v_3 が反時計回りに見える方向に飛び出す」という性質があります。上の図の左の四面体だと4の逆方向、右の四面体だと4の方向です。
つまり、 ((v_2-v_1)\times(v_3-v_1))\cdot(v_4-v_1) ※1これは3次の行列式と深く関係しています の符号を見れば、四面体が反転しているかどうかが判別できます。左の四面体が正常で、右の四面体が反転したものとすると、
・ ((v_2-v_1)\times(v_3-v_1))\cdot(v_4-v_1)>0 ならば v_1 と v_2 を入れ替える
という処理を挟めば、反転した四面体も正常に処理できるようになります。
以上に気を付けると、全体の疑似コードは次のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
// 線分と原点の最接近点を返す Vec3 getClosestPointOnSegment(Vec3 v1, Vec3 v2) { // (略) } // 三角形の法線ベクトルを返す Vec3 getTriangleNormal(Vec3 v1, Vec3 v2, Vec3 v3) { return cross(v2 - v1, v3 - v1); } // 三角形と原点の最接近点を返す Vec3 getClosestPointOnTriangle(Vec3 v1, Vec3 v2, Vec3 v3) { Vec3 n = getTriangleNormal(v1, v2, v3); Vec3 n12 = cross(v2 - v1, n); Vec3 n23 = cross(v3 - v2, n); Vec3 n31 = cross(v1 - v3, n); boolean outer12 = dot(-v1, n12) > 0; boolean outer23 = dot(-v2, n23) > 0; boolean outer31 = dot(-v3, n31) > 0; Vec3 on12 = v1; Vec3 on23 = v1; Vec3 on31 = v1; if (outer12) { // 辺12上 on12 = getClosestPointOnSegment(v1, v2); } if (outer23) { // 辺23上 on23 = getClosestPointOnSegment(v2, v3); } if (outer31) { // 辺31上 on31 = getClosestPointOnSegment(v3, v1); } if (outer12 || outer23 || outer31) { // 辺上 return min(on12, on23, on31); } else { // 三角形上 return dot(v1, n) / dot(n, n) * n; } } // 四面体と原点の最接近点を返す Vec3 getClosestPointOnTetrahedron(Vec3 v1, Vec3 v2, Vec3 v3, Vec3 v4) { float det = dot(cross(v2 - v1, v3 - v1), v4 - v1); if (det > 0) { // 四面体が反転しているので、どれか2頂点を入れ替える swap(v1, v2); } Vec3 n123 = getTriangleNormal(v1, v2, v3); // 面 1→2→3 の法線ベクトル Vec3 n134 = getTriangleNormal(v1, v3, v4); // 面 1→3→4 の法線ベクトル Vec3 n142 = getTriangleNormal(v1, v4, v2); // 面 1→4→2 の法線ベクトル Vec3 n243 = getTriangleNormal(v2, v4, v3); // 面 2→4→3 の法線ベクトル boolean outer123 = dot(-v1, n123) > 0; boolean outer134 = dot(-v1, n134) > 0; boolean outer142 = dot(-v1, n142) > 0; boolean outer243 = dot(-v2, n243) > 0; Vec3 on123 = v1; Vec3 on134 = v1; Vec3 on142 = v1; Vec3 on243 = v1; if (outer123) { on123 = getClosestPointOnTriangle(v1, v2, v3); } if (outer134) { on134 = getClosestPointOnTriangle(v1, v3, v4); } if (outer142) { on142 = getClosestPointOnTriangle(v1, v4, v2); } if (outer243) { on243 = getClosestPointOnTriangle(v2, v4, v3); } if (outer123 || outer134 || outer142 || outer243) { // 三角形上 return min(on123, on134, on142, on243); } else { // 四面体内 return Vec3(0, 0, 0); } } |
注釈
| 1. | ↑ | これは3次の行列式と深く関係しています |