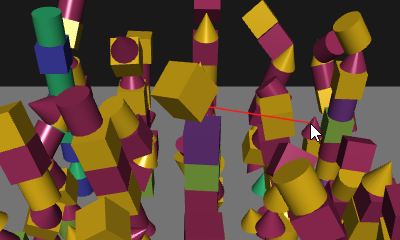
物理エンジンにレイキャストを実装したときの覚え書きです。
球、直方体、円柱、円錐とレイ(半直線)の交点と法線ベクトルを求めます。
共通事項
レイと基本図形の交差判定を行うにあたって、共通している点をまとめます。
レイの表現方法
いずれの判定でも、レイは始点ベクトル p と方向ベクトル d (特に正規化されている必要はありません)で表し、レイ上の点は p+td(t\geq0) とおきます。
こうすると、レイとの交点を求める問題が非負実数 t を求める問題に帰着されます。
図形の回転・平行移動
図形が回転・平行移動している場合、そのままでは交点を求めるのが難しくなることがあります。そのため、一度逆変換で回転・平行移動なしの座標系に持っていき、レイとの交点を求めたあとで元の座標系に戻してやります。そのため、以下ではすべて原点中心で回転なしの図形のみを扱います。
球とレイの交差判定
まずは一番簡単な球から。
半径 r の球を考えます。レイ上の点 p+td が球面上にある条件は、 |p+td|^2=r^2 です。変形すると
になります。ただの二次方程式ですので、これを解いてやりましょう。
ただし、このままでは扱い辛いので、 A=|d|^2,\ B=p\cdot d,\ C=|p|^2-r^2 などと置き換えてから解くとよいでしょう。
さて、これは二次方程式ですので、解が複数あったりなかったりします。正の解がない場合は交差無しでいいのですが、正の解が2つあった場合は小さい方を交点としましょう。なぜなら小さい方の解が球の内部に侵入する点を表すからです。
また、(単位)法線ベクトルは
となります。

直方体とレイの交差判定
各面が軸に平行な直方体に関する衝突判定では、直方体を各軸方向に分解して考える方法が度々有用となります。レイとの交差判定でも、X, Y, Z軸それぞれについてレイが直方体と交差する t の範囲を求め、それらの共通部分を取ることで最終的な t を求めます。
直方体のX, Y, Z軸方向の長さの半分をそれぞれ hw, hh, hd とおきます。
まず、X軸方向に関して直方体とレイが交差する条件は、
変形すると
\begin{aligned} \dfrac{-hw-p_x}{d_x}&\leq t\leq\dfrac{hw-p_x}{d_x} & (d_x>0)\\ \dfrac{hw-p_x}{d_x}&\leq t\leq\dfrac{-hw-p_x}{d_x} & (d_x<0)\\ -hw&\leq p_x\leq hw & (d_x=0) \end{aligned}3つも場合分けが出てきてしまいました。落ち着いて対処しましょう。
まず、 d_x=0 の場合ですが、この場合は -hw\leq p_x\leq hw が満たされないと分かった瞬間に判定を切り上げて脱出することができます。そうでなければ、レイは常に( -\infty<t<\infty で)X軸に関して直方体と重なります。
次に d_x\neq0 の場合ですが、これらはまとめて
\begin{aligned} \begin{array}{l} t_{x1}={\rm min}\{\dfrac{hw-p_x}{d_x},\dfrac{-hw-p_x}{d_x}\}\\ t_{x2}={\rm max}\{\dfrac{hw-p_x}{d_x},\dfrac{-hw-p_x}{d_x}\}\\ t_{x1}\leq t\leq t_{x2} \end{array} \end{aligned}と書くことができます。
同じ処理をY, Z軸に対しても行うことで、 t_{y1},t_{y2},t_{z1},t_{z2} を求めることができます。
\begin{aligned} t_{x1}&\leq t\leq t_{x2}\\ t_{y1}&\leq t\leq t_{y2}\\ t_{z1}&\leq t\leq t_{z2}\\ 0&\leq t \end{aligned}を満たす t が存在すれば、その最小値が求める t になります。
また、法線ベクトルは、レイが t_{x1},t_{y1},t_{z1} のうち最も大きいものに対応する軸方向から直方体に侵入すること、および方向ベクトル d の各成分の符号から求まります。

円柱とレイの交差判定
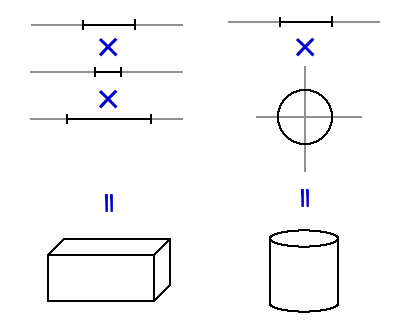
円柱とレイの交差判定は、直方体のときと同様に成分を分解して考えます。ただし、分解の仕方が直方体の場合と異なります。直方体は「3つの1次元上の区間の積」で表現できたのに対し、円柱は「1次元上の区間と円の積」で表現できます。
Y軸に平行な半径 r 、高さの半分 hh の円柱とレイの交差判定を考えます。
まず、高さ方向に対し、直方体と同じ方法で t の範囲を求めます。
ここでも、交差する可能性がなければ早期に判定を切り上げられることに注意してください。
次に、球と同じ方法で、XZ平面上に射影したレイ上の点が円の内部にあるような t の範囲を求めます。
\begin{aligned} |d_{xz}|^2t^2+2p_{xz}\cdot d_{xz}t+|p_{xz}|^2-r^2\leq 0 \end{aligned}ここで、XZ平面に射影している影響で、 d_{xz}=0 になる可能性があることに気をつけます。この場合、 |p_{xz}|^2<r^2 を満たせば常に交差、そうでなければ常に交差しません(早期脱出)。
d_{xz}\neq0 であれば、 t に関する2次方程式を解くことで、円と交差する t の範囲が求まります。これを
\begin{aligned} t_{xz1}\leq t\leq t_{xz2} \end{aligned}とします。
最後に、 t_{y1},t_{y2},t_{xz1},t_{xz2} の大小を比較して最終的な t を決定します。求める t は、
\begin{aligned} t_{y1}&\leq t\leq t_{y2}\\ t_{xz1}&\leq t\leq t_{xz2}\\ 0&\leq t \end{aligned}を満たす中での最小値になります。法線ベクトルは、直方体の場合と同様に t_{y1}\geq t_{xz1} であれば天面または底面から、 t_{y1}\leq t_{xz1} であれば側面からレイが侵入することから求まります。

円錐とレイの交差判定
これが一番厄介です。考え方としては直方体・円柱の場合と同じなのですが、錐と交差する t の範囲で場合分けがかなり出てきます。地道に潰していく以外の方法が思いつかなかったので地道にやりますが、賢い方法を誰か知っていたらぜひ教えてください。
円錐は、頂点が原点にあり、Y軸負の方向に向かって長さ h だけ伸びており、底面の半径が r であるとします。
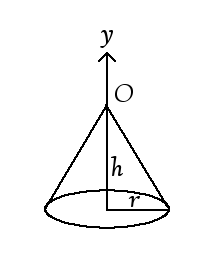
まず、高さ方向を円柱と同じように考え、交差する t の範囲を求めます。
\begin{aligned} \begin{array}{l} t_{y1}={\rm min}\{\dfrac{-p_y}{d_y},\dfrac{-h-p_y}{d_y}\}\\ t_{y2}={\rm max}\{\dfrac{-p_y}{d_y},\dfrac{-h-p_y}{d_y}\}\\ t_{y1}\leq t\leq t_{y2} \end{array} \end{aligned}次に、錐と交差する t の範囲を求めます。点 v が錐の内部にある条件は、
\begin{aligned} \dfrac{v_y^2}{|v|^2}\geq\dfrac{h^2}{h^2+r^2} \end{aligned}です。ただし、ここでの錐は円錐ではなく、下図のように上下方向に無限に伸びたものを指します※1こういう曲面のことを二次曲面といいます。一般に、二次曲面とレイの交差判定は高々2次の方程式を解くことで求めることができます。。
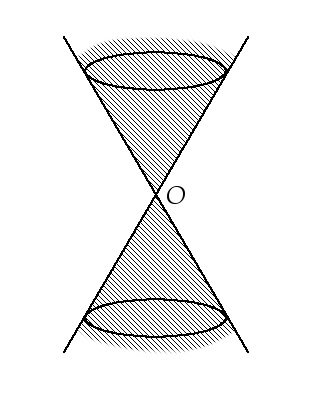
この錐と交差する t の範囲を求められれば、先程の t_{y1},t_{y2} と合わせることで円錐と交差する t の範囲を知ることができます。
先程の式に v=p+dt を代入し、 t に関して整理すると次のようになります。
\begin{aligned} (\dfrac{h^2}{h^2+r^2}|d|^2-d_y^2)t^2+2(\dfrac{h^2}{h^2+r^2}p\cdot d-p_yd_y)t+\dfrac{h^2}{h^2+r^2}|p|^2-p_y^2\leq0 \end{aligned}見た目がヤバい感じになっていますが、 t に関する方程式と思ってしまえば、ごちゃごちゃした部分はただの係数に過ぎないので
\begin{aligned} A&=\dfrac{h^2}{h^2+r^2}|d|^2-d_y^2\\ B&=\dfrac{h^2}{h^2+r^2}p\cdot d-p_yd_y\\ C&=\dfrac{h^2}{h^2+r^2}|p|^2-p_y^2 \end{aligned}と置き換えて
\begin{aligned}
At^2+2Bt+C\leq0
\end{aligned}
(交点では不等号が等号に変わります)
を解くことを考えます。以下、この方程式が実解を持つとします。実解を持たない場合は、レイと円錐は交差しないため、例によって判定を脱出します。
・ A>0 のとき
絶対値の十分大きな t は At^2+2Bt+C\leq0 を満たしません。したがって、錐と交差する t の範囲は、2つの解の間
\begin{aligned} \dfrac{-B-\sqrt{B^2-AC}}{A}\leq t\leq\dfrac{-B+\sqrt{B^2-AC}}{A} \end{aligned}です。
・ A<0 のとき
絶対値の十分大きな t は At^2+2Bt+C\leq0 を満たします。したがって、錐と交差する t の範囲は、2つの解の外側
\begin{aligned} -\infty<t\leq\dfrac{-B-\sqrt{B^2-AC}}{A} \end{aligned}または
\begin{aligned} \dfrac{-B+\sqrt{B^2-AC}}{A}\leq t<\infty \end{aligned}です。しかし、区間が「または」で2つに分割されていると、Y方向の区間との共通部分を求めるのが困難になってしまいます。そこで、この時点でどちらの区間が正しいか絞り込みを行います。
この場合分けに対応するのは以下の図のようなときです。赤丸が方程式の解に対応します。
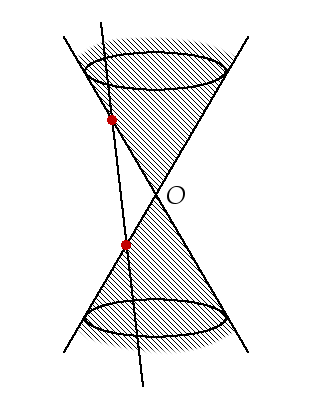
ここで、実際に円錐を構成するのは錐の下半分であることを思い出すと、錐の上半分に対応する区間は無視しても構わないことが分かります。
ではどちらの区間が下半分と交差するか?という問題になりますが、これはレイの方向ベクトル d のY成分を見ることで判別できます。
・ d_y>0 のとき、レイは上に向かって進むため、 -\infty を含む方が錐の下半分と交差します。
・ d_y<0 のとき、レイは下に向かって進むため、 \infty を含む方が錐の下半分と交差します。
以上で、二つあった区間を一つに絞ることができました。
・ A=0 のとき
この場合、方程式は二次ではなく一次だったことになります。このとき交点は一つで、 B の符号によって場合分けが生じます。
\begin{aligned} -\dfrac{C}{2B}&\leq t<\infty &(B<0)\\ -\infty&<t\leq-\dfrac{C}{2B} &(B>0) \end{aligned}
結局、どの場合においても、錐と交差する t の範囲
\begin{aligned} t_{c1}\leq t\leq t_{c2} \end{aligned}が求まります※2 \pm\infty が発生した場合は、適当な値でバウンドするか、適宜不等式の等号を消して読み替えてください。。ここまで来れば、後は円柱の場合と全く同じで
\begin{aligned} t_{y1}&\leq t\leq t_{y2}\\ t_{c1}&\leq t\leq t_{c2}\\ 0&\leq t \end{aligned}を満たす t の最小値を求めれば、それが円錐とレイの交点になります。

注釈
| 1. | ↑ | こういう曲面のことを二次曲面といいます。一般に、二次曲面とレイの交差判定は高々2次の方程式を解くことで求めることができます。 |
| 2. | ↑ | \pm\infty が発生した場合は、適当な値でバウンドするか、適宜不等式の等号を消して読み替えてください。 |