PCやスマートフォンのブラウザ上で動くリバーシ(オセロ)AIを作りました。
棋譜の読み込み・優劣のグラフ表示機能があるので対局の研究に使えます。
>> Run Application (HTML5+JS)
使い方
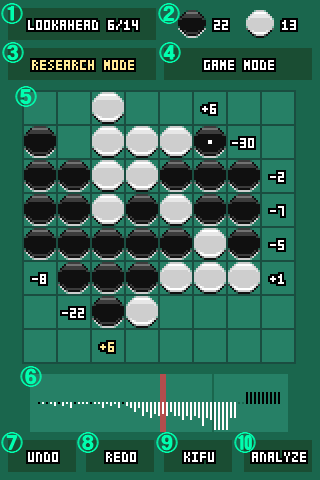
① 先読みの深さです。前半の数字は序盤・中盤の先読みの深さを、後半の数字は終盤の完全探索の深さを表します。クリックすることで読みの深さを変更できます。
② 現在の石の数です。
③ クリックすると研究モードに変わります。研究モードでは盤面に評価値が表示されます。
④ クリックすると対局モードに変わります。対局モードでは評価値は表示されず、相手の手番では自動的に石が置かれます。また、対局モード中にクリックすると自分の手番を変更することができます。
⑤ 盤面です。置ける箇所をクリックすると石を置くことができます。
⑥ 優劣を表すグラフです。ゲームを解析すると表示されるようになります。上向きに伸びていれば黒が、下向きに伸びていれば白が有利と予想されることを表します。グラフ中の赤いバーは現在のゲーム位置を、深緑のバーはそれ以降で完全読みが行われたことを表します。また、グラフをクリックすると対応する局面に飛ぶことができます。
⑦ クリックすると一つ前の局面に戻ります。
⑧ クリックすると一つ先の局面に進みます。
⑨ クリックするとゲームの棋譜を読み込むことができます。読み込み後はUNDO/REDOボタンが使えます。
⑩ クリックすると現在のゲームの解析を開始します。解析の精度は先読みの深さに依存します。解析が完了するとグラフが表示されるようになります。
強さ
最も弱い3手読みでも普通の人はまず勝てないです(自分も時々勝てるくらいです)。何人かに試してもらいましたが、4手読みの時点で初段以上の強さはあると思われます。6手読みと8手読みはよく分からないですが、同じ読みの深さでbook(定石データ)なしのZebraやEdaxといい戦いをしてくれました(あまり回数を試してないのでどちらが強いかは微妙ですが……)。
ただし、定石を学習させていないので序盤で正しく打たれるとやや弱いです。もしかしたら実装するかも。
以下、技術的な諸々の話です。
開発の経緯
ここ数ヵ月ほどリバーシにハマってしまい、空いた時間に遊ぶ日々が続いていました。最初はあまり気にしてなかったんですが、ある程度強くなるためには過去の自分の対局を分析して悪い手を探す作業が必要になります。
ここで必要になるのが分析に使うソフトウェアなのですが、PC版のものがほとんどなため、PCが使えない場所で対局を分析することができませんでした。対局のアプリはスマホ用なのに、これは悲しい。
……という訳で、スマホで動く研究用のリバーシAIを作ってやろうということになりました。
開発にあたって
以下のページには非常にお世話になりました。強いAIを作るためのノウハウやデータがよくまとめられています。
vsOtha アルゴリズム解説
Thell アルゴリズム解説
Reversi – bitboard and GPU computing
50万棋譜計画
使用したアルゴリズム等
非常にざっくりとした解説です。各種アルゴリズムの詳細は、先程紹介したページや他のサイトで多く解説されているので、詳しく知りたい方はそちらをご覧ください。
BitBoard
盤面を64ビット整数(あるいは32ビット整数2つ)で表現する手法。石が置ける場所の探索や、石をひっくり返す処理などをほぼ全てビット演算で行います。計算量のオーダーの改善はありませんが、普通にループで処理する場合に比べ圧倒的に速くなります。
パターン分解による評価値生成
優劣の評価関数を石の位置だけでなく、縦横のラインや辺などの分解されたパターン上にある石の並び方まで考慮して決定する手法。強いリバーシプログラムは大体この手法を使っています。
線形回帰による重み学習
膨大な数のパターン(横一列の並び方のパターンだけでも 38 = 6561 通り)に対する評価値(=重み)を、ある盤面に出現するパターンの評価値を足し合わせたときに、それが「両者が最善を尽くした場合の最終的な石差」になるべく近くなるように決定する手法。他の学習手法にはロジスティック回帰、深層学習などがあります。
評価関数のステージ分け
評価関数の精度を上げるため、ゲームの進行度によって複数の評価値を切り替えて使う手法。リバーシでは序盤と終盤で石の配置に対する優劣が大きく異なるため、同一の評価関数を使い続けるとどこかで精度が下がってしまいます。これを防ぐために、ゲームの進行度によって、同じパターンに対しても別々の評価値を割り当てます。
NegaMax法
ゲーム木の探索手法の一つで、αβ法に少し変更を加えたもの。シンプルに書けるのが特徴で、ここから更に派生するNegaScout法というアルゴリズムもあります。
置換表
ゲーム木の探索を効率化するため、一度探索したノードの評価値に関する情報を保存しておく手法。リバーシの場合、別々のルートを辿って同じノードに辿り着くことが多々あり、かなりの探索ノード数の削減を見込めます。後述のMTD(f)法を使う際には、置換表の実装がほぼ必須になります。
MTD(f)法
置換表とαβ法やNegaMax法を用いて最良優先探索的なことをする手法です。……プログラムはシンプルですが、解説が難しいので気になる方はご自身で調べてください。すいません。
(特に)使用していないアルゴリズム等
使ってもよかったが、面倒だったりして使われなかった手法です。
book
ゲーム序盤(場合によっては中盤、終盤まで)の進行に対する評価値を予めデータとして持っておく手法。いわゆる定石です。何だかんだで後回しにされた結果最後まで実装されませんでした。暇なとき実装するかも。
評価関数のスムージング
評価関数をステージごとに分けるときに、いきなり切り替えるのではなく段々に切り替えていく手法。ミップマップに対するトリリニアみたいな感じです。目立った境目が無いような気がしたので実装しませんでした。
ProbCut
αβ法やNegaMax法のような後ろ向き枝刈り(探索する必要性が全くないノードのみ探索を打ち切る)に対し、前向き枝刈り(恐らく探索する必要がないであろうノードも打ち切る)と呼ばれている種類の手法。パラメータ調整が難しく、下手に実装すると精度を下げる要因になるため今回は実装を見送りました。
Web上での公開にあたって
パターン数が膨大なため、評価関数のデータをそのままアップロードすると何十MBにもなってしまいます。そこで評価値を整数に直し、画像に埋め込んでpng形式でアップロードするようにしました。こうすることで冗長なデータが圧縮され、かつ読み込みもJavaScriptで簡単に行えるようになります。

読み込まれる画像の一つ
今更ですが、これ画像の幅を 3n になるように選ぶと圧縮効果が高まったのでは。
ソースコード
あまり綺麗なコードではありませんが、中身が見たい方向けにコアな部分のソースコードをここに置いておきます。Haxeで書かれています。

解析時間が短くても、かなり正確な手を打ってきて
双方最善に近い局面での対応力がずば抜けてますね!
さらに強化すればNtestクラスの強さになりそうな感じです。
“リバーシAIを作ってみた”是非このプログラムを見たいです。
ダウンドードは可能ですか。
よろしくお願いします。
AI部分のプログラムのソースコードはこちらに公開されています。
https://github.com/saharan/ReversiAI
ソースコード、拝見させていただきました!
理論的な説明は色んなサイトで見て回りましたが、実際にソースコードが公開されているところは少なかったので、参考にさせていただきました。
誠にありがとうございます。
一つお訊きしたいことがあるのですが、
AI部分のソースコードだけでは、実際にどのように実装されているのかが完全には理解できませんでした。
もしよろしければ、実際にゲームの実装に使われているソースコードも公開していただくことは可能でしょうか?
よろしくおねがいします。
ありがとうございます。
ゲーム部分のUIを含むプログラムは元々非公開の前提で書いていたので、かなりひどい感じのものになっていると思います(後でコードを探しておきますが、あまり期待はしないでください)
また、ゲームの方は基本的にAI部分のコードの関数を呼ぶ程度にしか使っていないです。現状公開されているAI部分のコードで、具体的にこの関数が何をやっているのかがわからない、このクラスは何をしているのか、などの疑問点がありましたら、コメントやTwitterで対象のソースコードを示してご質問をいただければ、回答できるかと思います。
ソースコード拝見させていただきました。
大変勉強になります。
Haxeというのも初めて触りましたが、とても簡単に色んな環境に移植できて良いですね。
1点質問があるのですが、
Gihubでライセンス等が見つかりませんでした。
こちらのソースコード(学習結果も含めて)は利用において制限や規約などはありますでしょうか?
可能であれば自作アプリに使用したいと考えています。
どうぞよろしくお願いいたします。
ありがとうございます。あまりきれいなコードではないですが参考になれば幸いです。
GitHub の方ではライセンスを付けておくのを忘れていました。なるべく自由に使っていただきたいので、MIT License を適用しておきました。
ご返信ありがとうございます。
edaxがわからなすぎて困っていたので、saharan様のコードが読みやすくて本当に助かりました。
MITライセンス助かります。
利用の際には一報入れさせていただきます。
ありがうございました。
失礼いたします。m(_ _)m
ソースコードを拝見させていただきました。大変参考になっております。一つ質問なのですが、JavaMain.hxを読むとL2正則化の定数(lambda)がステージが上がるに連れて小さくなっているのですが、このように定数を設定した意図があれば教えていただけると幸いです。
プログラムを見せてくださいお願いいつぃます