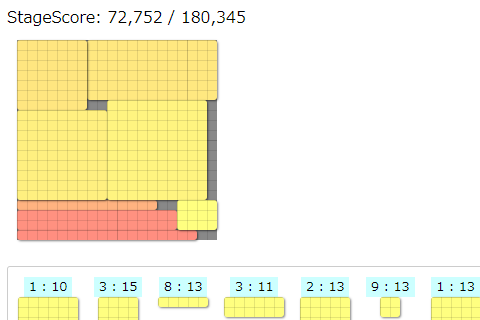
ハル研究所プログラミングコンテスト2018に参加しました。
初参加でしたが、なんとコンテスト終了時点で1位を取ることができました(11/15結果発表, ランキング)。
(11/15追記)
優勝しました!
以下参加記です。
問題
こちらにあります。簡単にまとめると
・長方形のクッキーの生地が流れてくるので、20×20マスのオーブンに詰め込んで焼く
・クッキーの形、焼きあがるまでの時間、獲得スコアはランダム※1ただし、ステージごとに(これもランダムに)事前に決められた確率分布に従います。
・1000ターン終了時までに焼きあがったクッキーの合計スコアが得点となる
というのを1ステージとして、20ステージの合計スコアを競うゲームです。プログラムは60秒以内に終了しなければなりません。
生地の大きさとスコア
生地が流れてくるレーンは2種類あり、小さい生地と大きい生地が常に8個ずつ存在するように補充され続けます。プレイヤーは好きな生地を選んでオーブンに置くことができますが、次にどんな生地が流れてくるかは分かりません(つまり、レーン内の16個しか見ることができません)。このように最初から全貌が見えない問題をオンライン問題といいます。これが今回の問題の非常に難しいところです。
また、大きい生地は小さい生地よりも焼きあがるのに時間がかかりますが、小さい生地より格段に高いスコアを獲得することができます。これより、小さい生地より大きい生地を優先して焼くべきであることが分かります。
基本方針
最終的なプログラムの基本方針は「配置順の全探索」になりました。クッキーは2次元で長方形ですが、焼きあがるまでに要するターン数を「クッキーの高さ※2実際には、焼きあがってから回収までに1ターンかかるため、必要なターン数+1がクッキーの高さになります。終盤までこれを見逃しており、バグを直したところスコアが6万点ほど伸びました。」として全ての生地を20×20×1000の大きさのオーブンに詰め込むことを考えると、3次元の直方体詰め込み問題になります。
3次元の直方体詰め込み問題を解くアルゴリズムとして、Bottom-Left法を3次元に拡張したものが知られています。箱を詰め込む順番を(何らかの方法で)決めておき、それぞれを配置可能な座標の中で
・もっとも深い場所に
・その中でも最も下側に
・さらにその中でも最も左側に
ある場所(このような点をBL点といいます)に置いていきます。
もしも箱が隙間なく詰め込める場合、上記の方法で隙間なく詰め込めるような順列が存在することが知られています。したがって、どうにかうまい順列を見つけることが今回の問題においてもスコアアップにつながると考えられます。
今回の問題では、生地を1つ配置するごとに新しい生地が補充されるため未来の正確な予測が不可能であり、z座標を「今からzターン後」と定めた場合、z座標が大きくなるにつれ不確かさが増加していきます。生成される生地の確率分布から未来を「推定」することはできますが、この手の離散最適化問題では「わずかなパラメータの変化が最適解を大きく変化させる」ことが往々にしてあり、有用な結果が得られる可能性は低いと思われることから未来の推定は行いませんでした。
遠い未来が不確かであるならば直近の未来から行動を決定するべきであり、したがって「直後に配置する n 個の生地の順列」を全探索する策を取りました。残りの生地は適当な順番で詰め込んでやります。
配置の高速化
全探索を行うためには、1つの順列の評価が高速に行われなければなりません。与えられた生地の順列からそれぞれの生地を配置するBL点を発見する部分がボトルネックになりますので、そこを重点的に高速化します。この辺りは本当に苦労したのですが、以下のような手法で高速化を図りました。基本的にビット演算マシマシです。
・long long 型の配列を使ってオーブンのビットボードを作ることで、クッキーを配置不可能な点を高速に列挙する
・popcountその他を使ってビットボードにおけるBL点を高速に検出する
・新しい生地が入ってこなかったターンは何も計算せず、前回の結果を使い回す
配置の評価
間違いなくこの問題における最難関です。前にも書いた通り、未来の正確な予測ができないため「現在の配置を完全に正しく評価する評価関数」を作ることができません。ではどうするかというと、直近の未来はそれなりに正しいことを利用して、現在に近い方から重みを付けて評価してやります※3これでも正しい評価ができるとは言い難く、わずかな重みの付け方の違いによって数万点単位でスコアが変動していました。。
また、あるz値の領域 [z_1,z_2] における点数の付け方ですが、各生地に対して領域 [z_1,z_2] と交差する体積の比率を求め、それにその生地の獲得スコアをかけて総和・・・
を取ってはいけません。これにしばらくの間気づかなかったのですが、この問題の罠の一つです。よくよく考えてみると、「焼かなかった生地は手元に残る」ため、流れてきたすべての生地のうち、焼かずにスルーできる生地は高々16個です。そのため、「スコアの最大化」は概ね「焼いた個数の最大化」と同一視することができます。
さらに、流れてくる生地が固定されているなら「生地の総体積」も固定されており、したがって「焼いた個数の最大化」を「充填率の最大化」と同一視することができます!
以上より、あるz値の領域 [z_1,z_2] における点数は、各生地に対して領域 [z_1,z_2] と交差する体積の総和にすべきことが分かります。これを「適当なz座標の分割」により「適当な重み付け」をして足し合わせたものを評価値とします。どう分割してどう重み付けするのが最適か全く分からないため、この辺りは本当に適当です。プロコン終盤ではこの辺のパラメータをひたすらいじってスコアが上がることを祈っていました。
大きい生地と小さい生地の扱い
大きい生地と小さい生地では獲得スコアが格段に違うため、大きい生地を優先して置くべきであることが分かっています。したがって、探索においては「大きい生地8個の最適な順列」をまず決め、その後「大きい生地を邪魔せずに置ける小さい生地8個の最適な順列」を求めます。これにより、全部の生地16個をまとめて考えるよりも計算量が減るというメリットもあります。
さらに、大きい生地に関する探索パラメータと小さい生地に関する探索パラメータを独立に調整できるため、「大きい生地に関して高いスコアが取れるパラメータを探す」→「小さい生地に関して高いスコアが取れるパラメータを探す」という風に2段階に分けてパラメータ調節を行うことができ、終盤でのゴリ押しスコアアップに繋がりました。
終盤の戦略
各ステージにおいて、終盤だけは「獲得スコアを考えて配置を評価する」ことが有利になります。というのも「最後に残す16ピースの選択」を行うことができるようになるからです。そのため終盤だけ評価関数を変化させ、「1000ターン以内に焼きあがる生地の総スコア」で評価するように変更しました。これで+4000点ほどスコアが伸びています。
結果
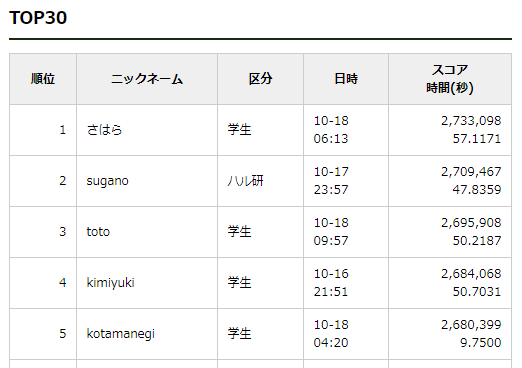
2位のsuganoさんに24,000点ほど差を付けて1位になることができました。終了2日前くらいまでは270万点台を出しているのが他にいなかったため若干安心していたのですが、突然suganoさんが4万点ほどスコアを伸ばして270万点台を叩き出したため非常に焦りました。怖かったです。最後に気合で2万点伸ばしました。
おまけ
kimiyukiさんとkurenai3110さんのやり取りが印象的でした
@kurenai3110 ハル研 抜いた
— うさぎ (@a3VtYQo) 2018年10月10日
↑当時1位だったkurenai3110さんを抜くkimiyukiさん
気のせいじゃないですか?
— くれない(21)。 (@kurenai3110) 2018年10月10日
↑2万点差を付けて抜き返したkurenai3110さん
いやそんなことないですよ。ちゃんとページ更新しましたか?
— うさぎ (@a3VtYQo) 2018年10月10日
↑さらに再び2万点差を付けて抜き返すkimiyukiさん
注釈
| 1. | ↑ | ただし、ステージごとに(これもランダムに)事前に決められた確率分布に従います。 |
| 2. | ↑ | 実際には、焼きあがってから回収までに1ターンかかるため、必要なターン数+1がクッキーの高さになります。終盤までこれを見逃しており、バグを直したところスコアが6万点ほど伸びました。 |
| 3. | ↑ | これでも正しい評価ができるとは言い難く、わずかな重みの付け方の違いによって数万点単位でスコアが変動していました。 |