物理エンジンのジョイントを作るときにオイラー角についてかなり悩んだので覚え書きです。一般的な回転行列の表現方法としてよく使われるオイラー角ですが、その分かり辛さや性質の悪さから嫌われ者となることもしばしばです。ここではオイラー角の分かり辛い点や性質の悪さ、そしてそんなオイラー角と少しでも仲良くなるために必要な理解を書いておきます。
オイラー角とは
回転行列 R をx軸周りの回転行列 R_x 、y軸周りの回転行列 R_y 、z軸周りの回転行列 R_z の合成 R=R_xR_yR_z で表したとき、各軸周りの回転角の組 (\alpha,\beta,\gamma) をオイラー角といいます。このとき、合成の順序はいろいろ考えられ、どの合成順序を選ぶかでオイラー角の値は変わってきます。
\begin{aligned} R=R_xR_yR_z\\ R=R_yR_zR_x\\ R=R_zR_xR_y\\ R=R_zR_yR_x\\ R=R_yR_xR_z\\ R=R_xR_zR_y \end{aligned}さらに、x軸→y軸→x軸のように同じ軸を2回使う※1この場合3回目の回転の回転軸は2回目までの回転によって回転しているため、結果として R は3つの自由度をもちます。場合もあり、それら
\begin{aligned} R=R_xR_yR_x\\ R=R_xR_zR_x\\ R=R_yR_xR_y\\ R=R_yR_zR_y\\ R=R_zR_xR_z\\ R=R_zR_yR_z \end{aligned}も合わせると12通りのオイラー角が存在することになります。ですので「オイラー角」とだけ言われるとどれのことか分かりません。このような混乱を避けるため、x軸 → y軸 → z軸の順で合成するオイラー角をx-y-z系のオイラー角などと呼ぶことがあります。
この記事では、以降明確な記述がない場合はx-y-z系のオイラー角を考えます。
ジンバルロック
オイラー角に対応するものとして、よくジンバルが挙げられます。
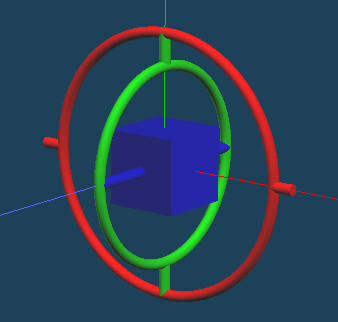
ジンバルは画像のように3つの回転軸で回転ができる機構で、真ん中の箱の回転行列を R とすると、赤色の部分が R_x に、緑色の部分が R_y に、青色の部分が R_z に対応します。適当に回してやると以下のようになります。
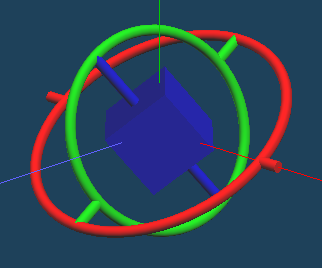
外側から順に、x軸で回転 → 回転後のy軸で回転 → 回転後のz軸で回転 となっていることが見て取れるかと思います。
さて、このジンバル付きの箱を手で持ってぐりぐりと回すことを考えてみてください。ジンバルは回転に関して3つの自由度を持つので特に問題なく回すことができるのですが、実はある状態に陥ると困ったことが発生します。
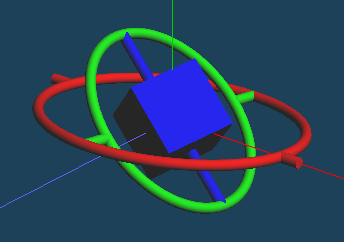
「ぐりぐりぐり~~」
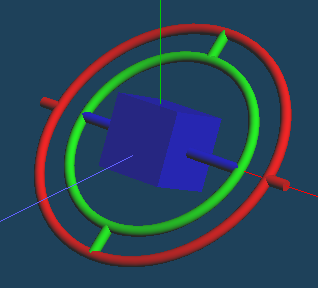
「あッ!!!!!」
よく見てください。回転のx軸とz軸が重なってしまいました。こうなるともはやジンバルの自由度は2になってしまうため、手で回せない方向が発生してしまいます。2つの円に垂直な軸方向にねじろうとしても回ってくれないことは明らかです。このような状態に陥ることを「ジンバルロック」といいます。オイラー角の持つ悪い性質の一つとされます。
一つ注意しておきたいのは、ジンバルロックが問題となるのはオイラー角を使って回転を「追跡」しようとする場合がほとんどであるということです。実は任意の回転行列はオイラー角を用いて表現できるので、オイラー角の表現力が足りなくて困るといったことは起こりません。
回転行列とオイラー角は一対一に対応するか?
しません。
まずジンバルロックを起こした場合ですが、中央の箱を固定して赤と緑の輪を同時にx軸=z軸にそって回すことで、同じ姿勢=回転行列※2姿勢と回転行列は一対一に対応します。に対して複数のオイラー角を無限に得ることができます。
次にジンバルロックを起こしていない場合ですが、実はこちらも一対一対応することはありません。
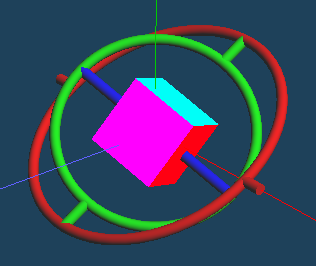
画像はオイラー角 (120^\circ, 60^\circ, 30^\circ) で回転させたときのジンバルの様子です。分かりやすいように箱に色を付けています。では、ここからx軸周りに180度ジンバルを回転させます。
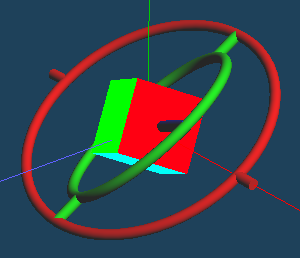
更に、y軸周りに60度回転させます。
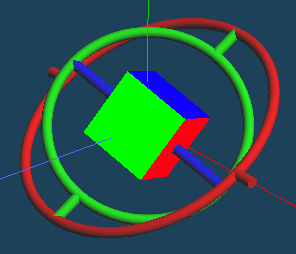
最後に、z軸周りに180度回転させます。

はい、元に戻りました。
・・・というのは嘘で、このときのオイラー角は (120^\circ+180^\circ,60^\circ+60^\circ,30^\circ+180^\circ)=(-60^\circ,120^\circ,-150^\circ) になっています。赤と緑のリングがそれぞれ裏返っている状態です。一般に、ジンバルロックを起こしていないオイラー角 (\alpha,\beta,\gamma) に対して、 (\alpha+180^\circ,180^\circ-\beta,\gamma+180^\circ) は同じ姿勢を表します。つまり1つの回転行列に対しオイラー角が2通り存在します。
ここで、 \beta\neq\pm90^\circ のとき( \beta=\pm90^\circ のときジンバルロックが起こることに注意)、 \beta と 180^\circ-\beta の少なくとも一方のみが \pm90^\circ 以内に入っています。したがって、 |\beta|<90^\circ という制限を設ければ、オイラー角と回転行列は一対一に対応することになります!
この「一対一に対応する」という条件は、回転行列からオイラー角を逆算するときに非常に重要になります。
回転行列からオイラー角を求める
オイラー角を扱う人が最も苦戦するであろう問題の一つがこの 回転行列 → オイラー角の変換 ではないでしょうか。ここでは実際に回転行列からオイラー角を求めていきます。
まず、オイラー角 (\alpha,\beta,\gamma) から回転行列を求めます。x軸周りの回転行列 R_x は
\begin{aligned} R_x=\begin{pmatrix} 1 & 0 & 0\\ 0 & \cos\alpha & -\sin\alpha\\ 0 & \sin\alpha & \cos\alpha \end{pmatrix} \end{aligned}同様に、y軸、z軸周りの回転行列は
\begin{aligned} R_y=\begin{pmatrix} \cos\beta & 0 & \sin\beta\\ 0 & 1 & 0\\ -\sin\beta & 0 & \cos\beta \end{pmatrix}\\ R_z=\begin{pmatrix} \cos\gamma & -\sin\gamma & 0\\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{pmatrix} \end{aligned}です。これらを合成すると回転行列 R が得られます。
\begin{aligned} R=R_xR_yR_z=\begin{pmatrix} \cos\beta\cos\gamma & -\cos\beta\sin\gamma & \sin\beta\\ \cos\alpha\sin\gamma+\cos\gamma\sin\alpha\sin\beta & \cos\alpha\cos\gamma-\sin\alpha\sin\beta\sin\gamma & -\cos\beta\sin\alpha\\ \sin\alpha\sin\gamma-\cos\alpha\cos\gamma\sin\beta & \cos\gamma\sin\alpha+\cos\alpha\sin\beta\sin\gamma & \cos\alpha\cos\beta \end{pmatrix} \end{aligned}一見複雑な形になりましたが、 R の1行3列成分に注目してみましょう。
\begin{aligned} R_{1,3}=&\sin\beta \end{aligned}この式に注目すると、 R がジンバルロックを起こしているかどうかが分かります。ジンバルロックが発生するのは \beta=\pm90^\circ のときだったので、そのときの \sin\beta の値は \pm1 になります。すると \cos\beta の値は 0 となり、 R は次のように単純化されます。
\begin{aligned} R=\begin{pmatrix} 0 & 0 & \pm1\\ \cos\alpha\sin\gamma\pm\cos\gamma\sin\alpha & \cos\alpha\cos\gamma\mp\sin\alpha\sin\gamma & 0\\ \sin\alpha\sin\gamma\mp\cos\alpha\cos\gamma & \cos\gamma\sin\alpha\pm\cos\alpha\sin\gamma & 0 \end{pmatrix} \end{aligned}ここで三角関数の加法定理を用いると
\begin{aligned} R=\begin{pmatrix} 0 & 0 & \pm1\\ \pm\sin(\alpha\pm\gamma) & \cos(\alpha\pm\gamma) & 0\\ \mp\cos(\alpha\pm\gamma) & \sin(\alpha\pm\gamma) & 0 \end{pmatrix} \end{aligned}となるので、 \sin(\alpha\pm\gamma) 、 \cos(\alpha\pm\gamma) が分かり、これより \alpha\pm\gamma が一意に定まります。 \alpha\pm\gamma=C を満たすような \alpha と \gamma は無限に存在するので、 R に対応するオイラー角は無限に存在します( \gamma=0 などの仮定を置いてやることで、そのうちの一つを求めることができます)。
では \sin\beta\neq\pm1 の場合を考えましょう。このとき R はジンバルロックを起こしていないので、 |\beta|<90^\circ に限定すればオイラー角は一意に定まります。まず、値域が \pm90^\circ 以内である逆三角関数 \sin^{-1} を用いて
\begin{aligned} \beta=\sin^{-1}R_{1,3} \end{aligned}とします。すると \cos\beta\neq0 ですから、
\begin{aligned} R/\cos\beta=\begin{pmatrix} \cos\gamma & -\sin\gamma & *\\ * & * & -\sin\alpha\\ * & * & \cos\alpha \end{pmatrix} \end{aligned}となります。 * はどうでもいい値です。これより、 \sin\alpha,\cos\alpha,\sin\gamma,\cos\gamma が分かり、したがって \alpha,\gamma が一意に定まります。なお、 |\beta|>90^\circ に対応するもう一つのオイラー角は (\alpha+180^\circ,180^\circ-\beta,\gamma+180^\circ) となります。
以上のように、 \sin\beta の値に応じて場合分けしてやることで、回転行列 R に対応するオイラー角をすべて求めることができます。x-y-z系以外のオイラー角についても、全て同様の手法で求めることができます。「求め方」を知っていることは「公式」を知っていることよりも遥かに価値があるのです。
ここまで読むと「オイラー角って性質が悪い上に扱いにくくて嫌だな……」と思う人が多いのも納得できるかと思います。ですが、そんなオイラー角にも実は数学的に綺麗な一面があります。
相対回転としてのオイラー角
ここからは少し難しい話になりますが、2つの回転行列をつなぐ回転(相対回転)としてのオイラー角の性質を見ていきます。
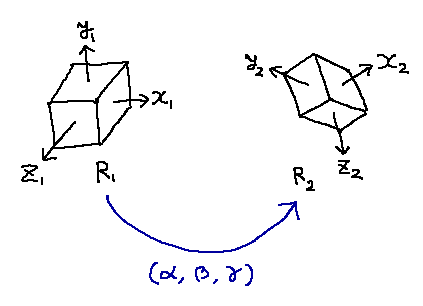
いま、2つの剛体があり、それぞれの姿勢が回転行列 R_1,R_2 で表されるとします。また、剛体1の基底※3ここでは剛体に沿ったx軸,y軸,z軸を表すベクトルの組のことです。を (x_1,y_1,z_1) 、剛体2の基底を (x_2,y_2,z_2) とします。ベクトルを列ベクトルとして扱えば、
\begin{aligned} R_1=\begin{pmatrix} x_1 & y_1 & z_1 \end{pmatrix}\\ R_2=\begin{pmatrix} x_2 & y_2 & z_2 \end{pmatrix} \end{aligned}の関係が成り立ちます※4 (a,b) はベクトルの組で \begin{pmatrix}a&b\end{pmatrix} はベクトルの座標を横に結合した行列であることに注意してください。。これは標準基底
\begin{aligned} (e_x=\begin{pmatrix}1\\0\\0\end{pmatrix}, e_y=\begin{pmatrix}0\\1\\0\end{pmatrix}, e_z=\begin{pmatrix}0\\0\\1\end{pmatrix}) \end{aligned}を R_1,R_2 によって変換するとそれぞれ (x_1,y_1,z_1),(x_2,y_2,z_2) が得られることから分かります。
このとき、剛体1の立場から剛体2を見たときの回転行列を R とします。すると R は次のような連続する3回転の結合で表すことができます。
- x_1 周りに \alpha 回転させる。これにより (x_1,y_1,z_1) は (x'_1,y'_1,z'_1) に写される。
- y'_1 周りに \beta 回転させる。これにより (x'_1,y'_1,z'_1) は (x''_1,y''_1,z''_1) に写される。
- z''_1 周りに \gamma 回転させる。これにより (x''_1,y''_1,z''_1) は (x_2,y_2,z_2) に写される。
ここで、ベクトル a を a 周りに回転させても変化しないことから x'_1=x_1,y''_1=y'_1,z''_1=z_2 が成り立つので、次のように書き換えることができます。
- x_1 周りに \alpha 回転させる。これにより (x_1,y_1,z_1) は (x_1,y',z') に写される。
- y'_1 周りに \beta 回転させる。これにより (x_1,y',z') は (x',y',z_2) に写される。
- z_2 周りに \gamma 回転させる。これにより (x',y',z_2) は (x_2,y_2,z_2) に写される。
y' がどこに存在するかを考えてみましょう。上の手順をよく見ると、 y' は次の2通りの方法で得られることが分かります。
- y_1 を x_1 周りに \alpha 回転させる。
- y_2 を z_2 周りに -\gamma 回転させる。
1つ目の方法より、 y' は x_1 と直交する平面上にあることが分かり、2つ目の方法より、 y' は z_2 と直交する平面上にあることが分かります。したがって y' は x_1,z_2 のどちらとも直交します。これはすなわち y' が外積 x_1\times z_2 に平行であることを意味します。
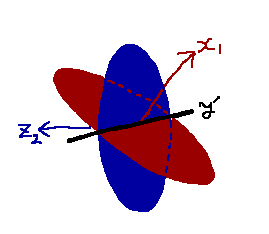
こうしてみると、オイラー角の回転軸が剛体1と剛体2の基底について対称的になっていることに気づきませんか?最初の回転軸は剛体1の基底から、最後の回転軸は剛体2の基底から、そして中間の回転軸は最初と最後の回転軸のどちらとも直交するベクトルから選ばれます。さらにこのことはx-y-z系のオイラー角に限らず成り立ちます※5例えばx-y-x系の場合、剛体1と剛体2から共にx軸の基底が選ばれ、z-x-y系の場合、剛体1の基底からz軸、剛体2の基底からy軸が選ばれます。。この対称性こそがオイラー角のもつ美しさの一つなのではないかと思います。
また、ジンバルロックの発生条件も対称的です。既に気づいた方もいるかもしれませんが、外積 x_1\times z_2=0 となるときがジンバルロックの発生条件です※6x-y-z系以外の系に対しても、最初と最後の回転軸が重なってしまった場合として説明できます。つまり、x-y-x系とx-z-x系のジンバルロックの発生条件は同一です。。この場合、最初に x_1 軸周りに何度回転させようとも、その後 y' 軸周りに \pm90^\circ 回転させさえすれば z_1 を z_2 に持っていくことができます。
最後に相対回転のオイラー角 (\alpha,\beta,\gamma) を求める方法です。 R は「剛体1から見た剛体2の回転行列」ですから、 R の1列目は「剛体2の基底のx軸(= x_2 )の、剛体1の基底(= (x_1,y_1,z_1) )による座標」です。すなわち、 R の1列目は
\begin{aligned} \begin{pmatrix} x_1\cdot x_2\\ y_1\cdot x_2\\ z_1\cdot x_2 \end{pmatrix} \end{aligned}になるはずです。ベクトルを列ベクトルと見なして内積を行列の積に置き換えると次のように書き直せます。
\begin{aligned} \begin{pmatrix} x_1\cdot x_2\\ y_1\cdot x_2\\ z_1\cdot x_2 \end{pmatrix} =\begin{pmatrix} x_1^T x_2\\ y_1^T x_2\\ z_1^T x_2 \end{pmatrix} &=\begin{pmatrix}x_1 & y_1 & z_1\end{pmatrix}^Tx_2\\ &=R_1^Tx_2\\ &=R_1^{-1}x_2 \end{aligned}回転行列に関しては転置と逆行列が等しくなる※7転置が元の行列の逆行列となるような行列を直交行列といいますが、「直交行列ならば回転行列」は成り立ちません。ことに注意してください。同様に R の2列目と3列目はそれぞれ R_1^{-1}y_2,R_1^{-1}z_2 となるので、
\begin{aligned} R&=\begin{pmatrix}R_1^{-1}x_2&R_1^{-1}y_2&R_1^{-1}z_2\end{pmatrix}\\ &=R_1^{-1}\begin{pmatrix}x_2&y_2&z_2\end{pmatrix}\\ &=R_1^{-1}R_2 \end{aligned}となります。後はこの R を先述の方法でオイラー角に変換してやれば、相対回転のオイラー角を得ることができます。
物理エンジンへの応用
2つの剛体の相対回転をオイラー角で制限するジョイントを作りました。ジョイントを作るとなると、上に書いた以外にも特異点付近での挙動の不安定性など色々問題が発生するのですがここでは省略します。

このジョイントはBullet PhysicsのGeneric6DoFJointと同じものです。自在継手(ユニバーサルジョイント、モップの先端についてるアレです)や車のタイヤに使われるジョイント(Hinge2Jointと呼ばれたりもします)などがオイラー角の拘束によって実現できます。意外と身近な場所にオイラー角は存在するんですね……!
注釈
| 1. | ↑ | この場合3回目の回転の回転軸は2回目までの回転によって回転しているため、結果として R は3つの自由度をもちます。 |
| 2. | ↑ | 姿勢と回転行列は一対一に対応します。 |
| 3. | ↑ | ここでは剛体に沿ったx軸,y軸,z軸を表すベクトルの組のことです。 |
| 4. | ↑ | (a,b) はベクトルの組で \begin{pmatrix}a&b\end{pmatrix} はベクトルの座標を横に結合した行列であることに注意してください。 |
| 5. | ↑ | 例えばx-y-x系の場合、剛体1と剛体2から共にx軸の基底が選ばれ、z-x-y系の場合、剛体1の基底からz軸、剛体2の基底からy軸が選ばれます。 |
| 6. | ↑ | x-y-z系以外の系に対しても、最初と最後の回転軸が重なってしまった場合として説明できます。つまり、x-y-x系とx-z-x系のジンバルロックの発生条件は同一です。 |
| 7. | ↑ | 転置が元の行列の逆行列となるような行列を直交行列といいますが、「直交行列ならば回転行列」は成り立ちません。 |