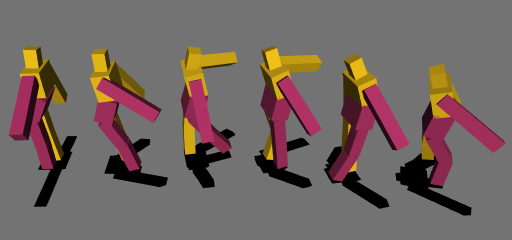
WebGLとCUDAで動く深層学習用のライブラリを作って深層強化学習 (Deep Deterministic Policy Gradient, DDPG) で二足歩行を学習させました。学習環境の作成にはOimoPhysicsを使いました。
開発の経緯や以下実装方法、学習結果などです。例によって怪しい個所へのツッコミは歓迎です。
これまでの流れ
前回の続きです。前回作ったプログラムを拡張してライブラリ化、その上で強化学習を行うプログラムを作成、WebGLとCUDAに対応させて二足歩行を学習といった流れになりました。
全結合NNから計算グラフへ
前回のプログラムでは全結合ニューラルネットワークに対する偏微分の計算方法をハードコーディングで実装していたため、全結合NN以外のモデルを使った学習ができませんでした。そこで、より一般的なモデルに対応できるよう計算グラフ(Computation Graph)に対して偏微分が計算できるようなプログラムを作成します。
計算グラフとはノード(頂点)が関数や変数、エッジ(辺)が入出力となるような有向グラフで、一連の計算の流れを表したものです。
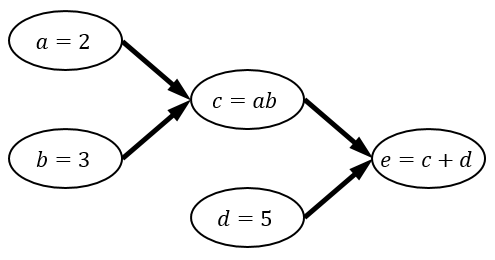
このグラフの e の値を計算したいとします。この場合、 e の入力に使われている c と d 、さらに c の入力に使われている a と b 、とグラフを遡って値を決定していきます。この操作を順伝播といい、これは単純な再帰関数などで書くことができます。
次にこのグラフの e による偏微分を計算したいとします。偏微分は全てのノードに対して求めます。すなわち、
\begin{aligned} \frac{\partial e}{\partial a},\frac{\partial e}{\partial b},\frac{\partial e}{\partial c},\frac{\partial e}{\partial d},\frac{\partial e}{\partial e} \end{aligned}をそれぞれ計算します。まず、 \dfrac{\partial e}{\partial e}=1 ですから、この値を決定します。次に、 e=c+d に注目します。 e は c と d に依存していますから、 \dfrac{\partial e}{\partial c},\dfrac{\partial e}{\partial d} の値が決定できます。ノード e は、ノード c と d にこれらの情報を渡します。この情報伝達はグラフの矢印と逆向きに行われるので、逆伝播と呼ばれます。
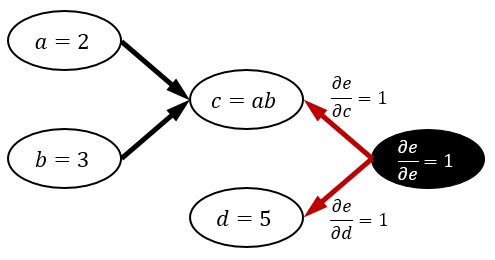
ノードから伸びている矢印全てから情報を受け取ったノードは、そのノードの微分係数を「受け取った情報の和」で確定できます※1これは微分の連鎖律 (chain rule) を反映しています。。この例ではノード c と d の微分係数がそれぞれ 1 で確定できます。微分係数が確定したノードは、そのノードで使われている変数の微分係数を計算し、再び矢印を逆向きに辿って情報を渡します。
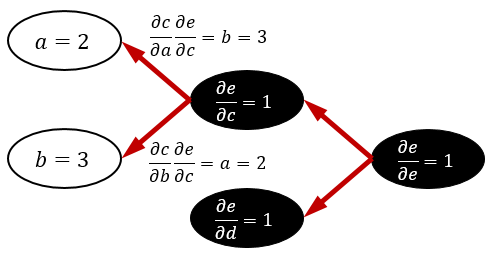
このとき、あるノードから渡す情報は図のように「ノードの入力変数による微分係数 \times 目的変数のノードによる微分係数」とします※2これも微分の連鎖律によるものです。実はノード e からは \dfrac{\partial e}{\partial c}\dfrac{\partial e}{\partial e} などが渡されていると考えても結果は変わらないので、場合分けは不要になります。。すると今度はノード a と b が全ての情報を受け取ったので、微分係数をそれぞれ b,a として確定できます。これで全ての変数による微分係数が求まりました。
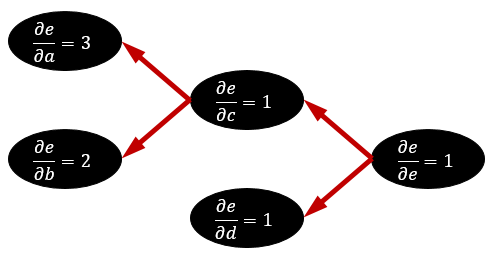
実際に実装する際には、
・あるノードがどこから参照されているかも必要な情報であること
・ e の計算に必要のないノードの微分係数は 0 とすること
・ノード e から幅優先探索を行えば微分係数が確定した順に逆伝播を行えること(参照のカウントは不要)
などに注意しつつプログラムを組むことになります。また、当然ですがノードの種類(加減乗除、指数・対数、絶対値、総和、平均、…などが考えられます)を増やせばそれらに対応した入力変数による偏微分係数の計算が必要になります。
高階微分はどうするの?
今回は実装しませんでしたが、一部の強化学習アルゴリズム(TRPOなど)では変数の2階微分が必要になります。これは、「偏微分係数を求めるための計算」を計算グラフとして構築する(!?)ことで可能になります。興味のある方は “double backpropagation” などで検索してみてください。簡単に手順を説明すると
・既存のグラフに「偏微分係数」を表す総和計算のノードを追加し、
・それらのノードに適切に情報が渡るようグラフを拡張する
という流れです。ただし、実装する演算全体の集合が「偏微分係数の計算に必要な演算を取る操作」について閉じている必要があります(でないと偏微分係数をグラフとして表せません)。この辺りの制約が厳しく、実装を見送ることになりました。
変数の高次元化
機械学習においては、後々計算を並列化するときに「1ノードの計算量をできるだけ大きくしたい!」という要求が出てきます。これはなぜかというと、
・1ノードの計算はGPUへの1つの命令で実行でき※3実際のところ1つでは済みませんが、ノードから伸びる辺の数を定数とすれば高々定数個です。まあ実質1つです。、並列度が高くなりうること
・GPUへの命令の送信、およびデータの転送に時間がかかること
あたりの理由があるためです。そのため、ノードに付随する変数をスカラーではなく多次元配列、いわゆるテンソルにしておくことには大きな意味があります。機械学習におけるミニバッチ学習では、変数の次元を元々の次元より1つ大きく持っておき、増えた次元にミニバッチ用の学習データを詰め込む、というのが定石と化しています。
変数を多次元にしても順伝播や逆伝播の本質的な計算方法は変わりません。が、実装が格段に面倒になります。今回実装したライブラリでは、GLSLで使えるベクトルの次元が4以下であったこともあり、4階までのテンソルのみ扱えるようにしました。
GPGPUで並列化する
上記の理由から、多次元変数の加減乗除、行列積やテンソル積を計算するノードを実装することになるのですが、これらはいい感じにGPUで並列計算することができます。WebGLを使う場合は変数を一度1次元に並べ直し、2次元のテクスチャに押し込んで保存しておくことでフラグメントシェーダを用いて並列計算ができます。恐らくいわゆるシェーダ芸と言われる類のもので、大変ですが原理上可能なので頑張ると実装できます。CUDAの場合はC言語ライクに書けるのでもうちょっと簡単ですが、NVIDIA社製のGPUが搭載されていないPCでは動きません。
そんなこんなでGPUに対応した深層学習用のライブラリができました。リポジトリはこちらにあります。次は強化学習の話です。
強化学習ことはじめ
今回実装した強化学習のアルゴリズムは DDPG (Deep Deterministic Policy Gradient) ですが、必要となる前提知識が多いので順を追って説明します。まず強化学習についてです。
強化学習では、ある環境に置かれたエージェントの行動を最適化する問題を解くことを考えます。エージェントは「動くモノ」くらいに思っておけば大丈夫です。エージェントは「環境」に対して取れる行動が決められていて、その中から1つを選び行動します。このとき、環境はエージェントの行動を受けて変化することがあります。また、エージェントは環境の一部を「観測」することができ、観測結果によって行動を決定することができます(すなわち、周りを見て行動を決めることができます)。ここで重要な点として、エージェントは行動の結果に対して「罰」または「報酬」を与えられます。ただし、どのようにして与えられる報酬が決まるのかについて直接知ることはできません。エージェントは「観測」「行動」「罰または報酬の受け取り」を繰り返しながら、より良い報酬が受け取れるように自分の行動を最適化していきます。
強化学習の利点として、「教師データがいらない」というのがあります。報酬の与え方さえ適切に設定すれば※4実はこれが大変難しいです。強化学習の罠です。、手本となるデータがなくともエージェントに行動を学習させることができます。この点は強化学習が「教師あり学習」とも「教師なし学習」とも異なる点です。
Q学習
さて強化学習が何をするのかは分かりましたが、実際にどうやって問題を解くのかがまだ分かりません。ここでは一般的に用いられる手法である「Q学習」について簡単に解説します。
まず、エージェントの行動を最適化するためには「最適な行動とは何か」を定義する必要があります。多くの場合、最適な行動は次の累積報酬の期待値を最大化する行動として定義されます。
\begin{aligned} \sum_{t=0}^\infty \gamma^tr_t=r_0+\gamma r_1+\gamma^2r_2+\cdots \end{aligned}ここで r_t は時刻 t において受け取った報酬※5負の報酬は罰を表します。で、 \gamma は割引率です。割引率とは「未来において受け取る報酬をどれだけ高く評価するか」を示す数値で、 \gamma=1 とすれば「今すぐ受け取る100円よりも8億年後に受け取る101円を優先する人」になり、 \gamma=0 とすれば「完全に目先の利益しか考えない人」ができあがることになります。基本的に将来のことを考えた方がいいのですが、 \gamma=1 とすると数値が発散してしまうことがあるので \gamma=0.95\sim0.99 くらいがよく用いられます。
次にQ関数を導入します。Q関数とは、現在の観測可能な状態 s と次に取る行動 a を受け取り、「いま行動 a を取り、それ以降は最適な行動を取り続けた場合に受け取れる累積報酬の期待値」を返します。これを Q(s,a) と書きます。Q関数の値(=Q値)は、直感的には「状態 s で行動 a を取ることがどれほど良いか」を表します。このQ関数が全ての状態と行動について求まれば、現在の状態において最もQ値が高くなる行動を取り続けることで目的を達成できます。
問題は「Q関数をどうやって求めるか?」ですが、そのためには次のQ関数の性質を使います。
\begin{aligned} Q(s_t,a_t)=r_t+\gamma\max_{a}\{Q(s_{t+1},a)\} \end{aligned}右辺の r_t は「状態 s_t で行動 a_t を取ったときに得られる報酬」で、 s_{t+1} は「状態 s_t で行動 a_t を取ったときの次の状態」です。なぜこの式が成り立つのかは、1秒だけ先読みするつもりでQ関数を見ると理解できるのではと思います。
さて、この式を使うと、「Q関数の見積もり」が手元にあったときに、「状態 s_t で行動 a_t を取って報酬 r_t を得た」という経験をもとに、Q関数の見積もりがどれだけ真のQ関数から外れているかを計算することができます。見積もりが正しいと仮定したときの Q(s_t,a_t) の値
\begin{aligned} r_t+\gamma\max_{a}\{Q(s_{t+1},a)\} \end{aligned}と実際の Q(s_t,a_t) を比較すればいいのです。これらの差
\begin{aligned} \left(r_t+\gamma\max_{a}\{Q(s_{t+1},a)\}\right)-Q(s_t,a_t) \end{aligned}をTD誤差 (temporal-difference error) といいます。このTD誤差が0になるようにQ関数の見積もりを少しずつ修正していけば、いずれ真のQ関数が得られるだろう※6実際には、TD誤差による修正を繰り返したときに真のQ関数に常に収束するわけではなく、様々な条件が必要となります。、というのがQ学習の大枠です。他にも、得られる経験が局所的にならないようにするためのε-Greedy法などの必要とされるテクニックがありますが、ここでは割愛します。
Deep Q-Network
いよいよ強化学習と深層学習を組み合わせます。先程の「Q関数の見積もり」にニューラルネットワークを使ってしまおうというのがDQN (Deep Q-Network) です。こう書くと簡単に見えますが、この試みは簡単に成功したわけではなく、愚直に実装するとネットワークの重みが発散してしまう問題についに解決策が見つかってこその成果でした。
問題の一つに、「時系列に沿ったデータで次々学習を行うとネットワークの重みが発散する」というものがあります。これは、状態 s_t 、行動 a_t 、得られた報酬 r_t 、次の状態 s_{t+1} の組 (s_t,a_t,r_t,s_{t+1}) を「経験」として保存しておき、過去の経験からランダムに取り出して学習を行う方法 (Experience Replay) により解決されました。経験をシャッフルして時系列に関する相関を打ち消してしまおうという考えです。この方法は深層強化学習において度々用いられ、DDPGもその例外ではありません。
もう一つの問題に、「手持ちのQ関数の近似でTD誤差を計算して学習するとネットワークの重みが発散するか、学習が全く進まなくなる」というものがあります。これはなぜかというと、Q関数の更新目標にQ関数自身の値を用いているためで、ニューラルネットワークではこれが原因で安定した更新ができなくなってしまいます。そのため、「更新目標とするQ関数のネットワークをもう一つ別に持っておき (Target Network) 、定期的に手持ちのQ関数の値で更新する」という手法が考案されました。これにより学習を安定化させ、ついにニューラルネットワークを用いてQ学習を行うことができるようになりました。ただし Target Network を用いた代償として、学習にかかる時間が倍増しています(それでも Target Network を使わないとそもそも正しく学習が進まないので、時間を掛ける価値は十分にあると思われます)。DDPGにおいても Target Network が使われています。
DQNの特徴は他にもありますので、こちらも興味がある方は調べてみてください。
連続行動空間への拡張
DQNを使う上での制約として、「エージェントの取れる行動が離散的である」というものがあります。つまりエージェントは
・上に進む
・下に進む
・左に進む
・右に進む
・足元を見る
・……
など有限の種類の中から選ぶ必要があり、
・力 f でジャンプする
など連続値を取る行動を学習することはできません。細かく分割すればできると言えばできるのですが、行動の総数が行動の種類と分割数に応じて指数関数的に増加していき現実的ではありません。例えば15個のモーターを制御しようと考えたとき、各モーターに「正転」「逆転」「フリー」の3種類の命令を送れるとすると、行動の総数は 3^{15}=14348907 になります。毎回 14348907 個のQ関数の出力を見て最大値を取るような行動を決めなければいけないわけですから、とてもやってられたものではありません。
しかし行動が連続空間から選べるとなると、先程のモーターの例では「各モーターのトルクを表す15次元の実数値ベクトル」を1つ出力すればいいことになります。これならいけそうです。
行動を連続空間に拡張する方法は大きく分けて2つあります。
・行動を生成する確率分布のパラメータを学習する方法
・直接連続行動空間から行動を出力する関数を学習する方法
どちらも方策勾配法 (Policy Gradient) に属する手法です。前者は確率的な手法であり、TRPO (Trust Region Policy Optimization) や PPO (Proximal Policy Optimization) などがこれにあたります。DDPG (Deep Deterministic Policy Gradient) は後者に属する手法であり、Deterministicとある通り決定的な行動関数を学習できるのが特徴です。
DDPG
ここでは方策勾配法の詳細については触れませんが、DDPGが何をやっているのかが分かるようにできるだけ簡単に説明します。
DDPGではActor NetworkとCritic Networkの2種類のネットワークを使います。Actor Networkはその名の通り行動を計算するためのネットワークで、「状態 s を受け取り取るべき行動 a を返す関数」です。一方Critic NetworkはActor Networkの計算した行動を評価するネットワークで、「状態 s と行動 a を受け取りQ値を返す関数」です。学習の際はActor NetworkがCritic Networkを参考に、Critic NetworkがActor Networkを参考にしつつ成長していきます。
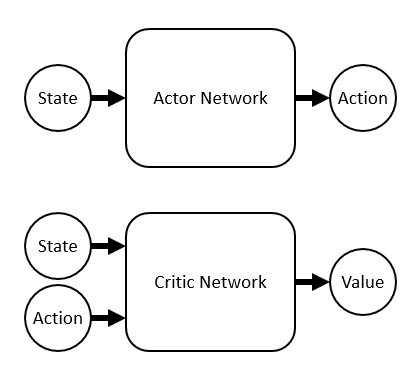
まずCritic Networkの学習方法ですが、Critic Networkは実質Q関数なので、Q学習の節で述べた方法が使えます。経験 (s_t,a_t,r_t,s_{t+1}) を用いて学習するとき、まずActor Networkで「Critic Networkが最大値を返すことが期待されている行動 a'_t 」を計算します。Actor Networkが正しいと仮定すれば、次が成り立ちます。
\begin{aligned} a'_t=\mathop{\mathrm{argmax}}\limits_a\{Q(s_t,a)\} \end{aligned}するとTD誤差が計算できます。
\begin{aligned} TD_{error}=(r_t+\gamma Q(s_t,a'_t))-Q(s_t,a_t) \end{aligned}実際には、DQNの節で説明したように a'_t と Q(s_t,a'_t) の計算には学習中のActor NetworkとCritic NetworkではなくそれぞれのTarget Networkを用います。このTD誤差を用いてCritic Networkを学習していきます。
次にActor Networkの学習方法ですが、ここがある意味DDPGの肝となっています。最終的な目標は、Critic Networkによる評価が上がるような行動をActor Networkが出力するように修正することです。
まずそれぞれのネットワークは微分可能でした。微分可能ということは、入力に対して出力が増加するようにパラメータを学習できるということです。Actor Networkは状態を受け取って行動を出力し、Critic Networkは状態と行動を受け取ってその状態におけるその行動の価値を計算します。
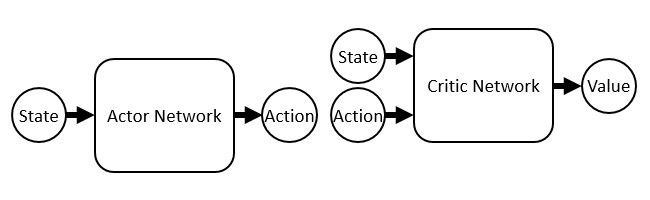
・・・
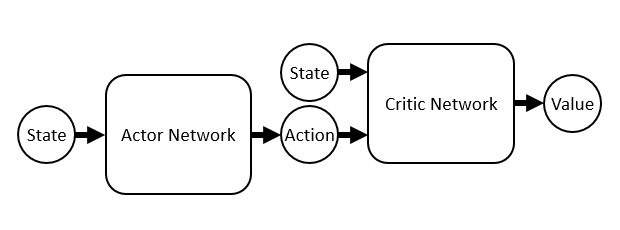
!
Actor Networkの出力とCritic Networkの入力を繋げてしまいました※7実際のところはネットワークを繋げるのではなく、求めるべき勾配が「Critic Networkの出力を行動で微分したものと、行動をActor Networkのパラメータで微分したものの積の期待値である (Deterministic Policy Gradient Theorem) 」という定理に基づいて計算します。しかしこれはネットワークを繋げて微分したときに得られる値の期待値と等しくなります(定理の証明にもQ関数と方策関数の合成の微分を用いているので、根底にある考え方は合っているのではないかと思います)。。するとどうでしょう。これらの構成要素は全て微分可能なので、Critic Networkの出力のActor Networkのパラメータによる偏微分
\begin{aligned} \frac{\partial\mathrm{Value}}{\partial\Theta_\mathrm{Actor}} \end{aligned}が計算できるではありませんか!これは「Critic Networkによる評価が上がるような行動をActor Networkが出力するようにパラメータを修正する方向ベクトル」に他なりません。この偏微分係数を使ってActor Networkを学習していきます。
以上が大変ざっくりとしたDDPGの説明ですが、より詳しく知りたい方はこちらのページ (Deep Deterministic Policy Gradients in TensorFlow) や原著論文 (Continuous control with deep reinforcement learning) を読んでみることをお勧めします。
以下は作成したプログラムで強化学習を行ってみた結果についてです。
振子の振り上げ問題
連続行動空間が要求される例としてよく挙げられるのがこの振り子の振り上げ問題です。強化学習のための環境を提供している OpenAI Gym には “Pendulum-v0” として実装されています。OpenAI Gymを使ってもよかったんですが、折角ライブラリを自作したので学習環境も自作しようということになりました。
振り子の振り上げ問題は、画像のように根元のモーター(何も見えませんがモーターがついてます)の出力を調整して振り子を振り上げ、そのまま静止させる問題です。画像は失敗して暴走しています。
モーターの出力は重力に負けるほど弱く、そのため出力を最大にしただけでは振り子を頂上まで持ち上げることができません。まずは一度逆方向に加速させて勢いをつけることが必要であり、さらに頂上で減速させ、バランスを保ち静止させなければなりません。この2点をうまく学習できるかが重要なポイントとなります。
最初は「ディープラーニングならこの位は余裕でいけるだろう」と思っていましたが、思わぬ落とし穴にはまることになります。
学習環境として、観測可能な状態を振り子の角度 \theta\in[-180^\circ,180^\circ] と角速度 \omega 、エージェントの行動はモーターのトルク、報酬は振り子の角度に応じて与えるよう調整しました。ネットワークは隠れ層の数が2、ユニット数が64と振り上げ問題に対しては恐らく十分であろう複雑さ※8後に同様のネットワークでの学習に成功しています。に設定しました。DDPGならきっと振り子を振り上げてくれるだろうと期待して学習が進むのを待ちましたが、一向に振り上げに成功する気配がありません。何をバグらせたのだろうと散々ソースコード内を探し回りましたが、原因は別のところにあったことが判明しました。観測可能な状態の与え方です。
観測可能な状態として \theta を与えていましたが、これは \pm180^\circ 地点で不連続な値を取ります。一方で、振り子の物理的な状態としては +180^\circ と -180^\circ は同一です。すなわち、物理的な状態とパラメータとしての状態に不連続な対応関係があり、これが学習の妨げとなっていました。OpenAI GymのwikiでPendulum-v0のページを見てみたところ、角度を \theta ではなく \cos\theta と \sin\theta で渡していました。つまり \theta そのものではなく、 \theta の方を向いた単位ベクトルを渡していたのです。確かにこれなら \pm180^\circ 地点でもパラメータとしての状態が滑らかに繋がります。同じように単位ベクトルを渡して再び学習させてみたところ、振り上げて静止することに成功しました。

左側の四角がActor Networkの出力、右側の四角がCritic Networkの出力を表します。左側の四角では横軸が角度、縦軸が角速度となっており、赤色が正のトルク、青色が負のトルクをモーターに与えることを意味します。右側は……すごく分かり辛いのですが「角度を固定したときの角速度とトルクとQ値」を表しています。横軸が角速度、縦軸がトルク、色がQ値に対応します。
ロボットの二足歩行
DDPGがきちんと動いていることが分かったので、いよいよ人型の二足歩行ロボットの学習に挑戦しました。
前回は倒れるだけだったロボット君ですが、体中にモーターを仕込み、剛体の重心、クォータニオン、速度、力積、関節の角度と速度を観測可能な状態に設定して学習を開始しました。
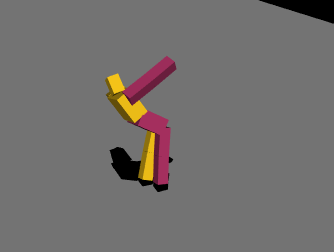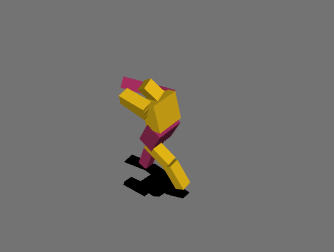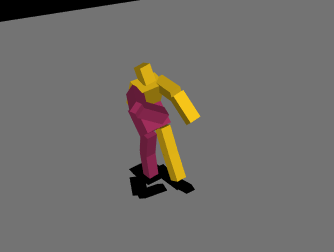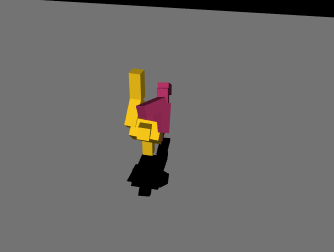
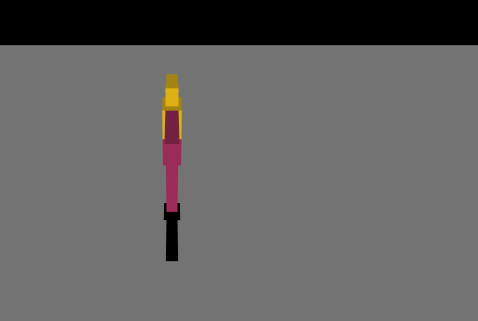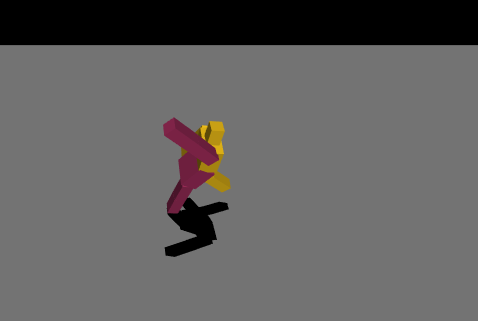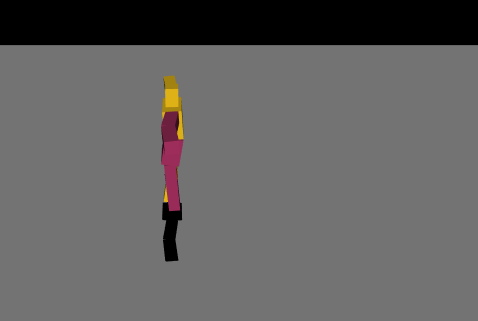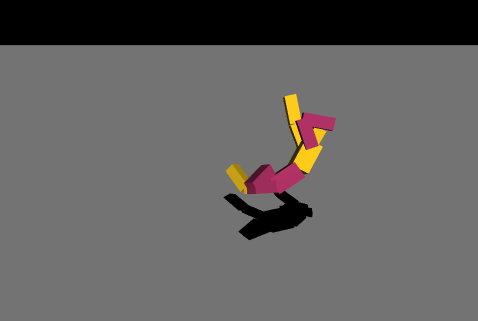
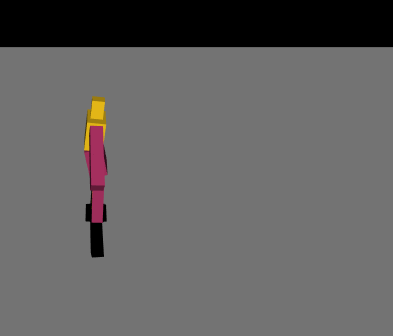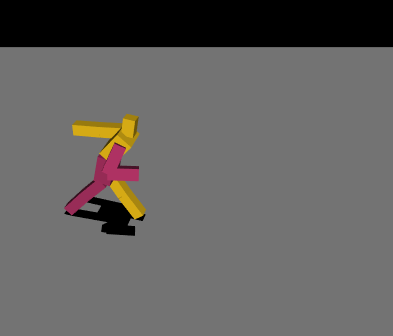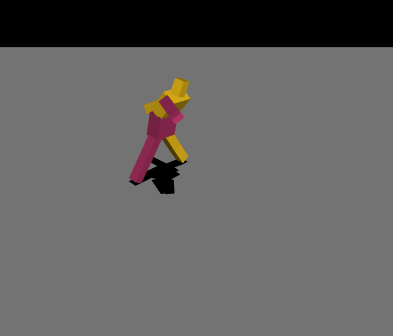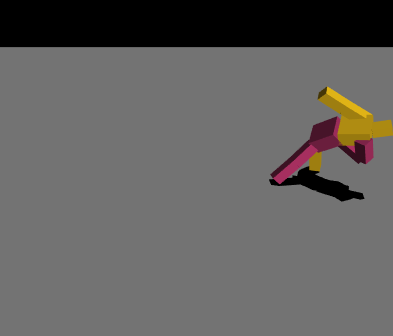
最初は絶望的な動きを繰り返していましたが、パラメータやネットワークの複雑さを変えて学習を繰り返し、ようやく少し歩けるようになりました。報酬の与え方を少し変えただけでも学習の進み方が全く変わってくるので学習環境を自作することの難しさを痛感しました……
そして先日、苦難の末ついにかなりの距離を歩行することに成功しました!

足取りはおぼつかないですが、倒れることなく前進しています。
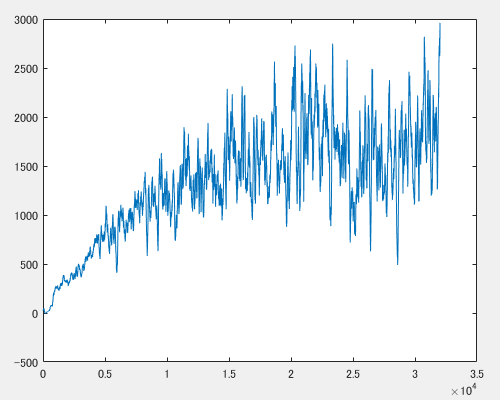
このときの学習曲線(横軸:エピソード数、縦軸:直近100エピソードの累計報酬の平均)です。途中から分散が大きくなっていますが、もう少し続ければまだ伸びるような気もします。ネットワークは隠れ層3、ユニット数600とかなり大きなものになってしまいました。OpenAI GymにあるHumanoidではもっと少ないパラメータ数での学習に成功している例があるので、もう少し減らせないものかと思っているのですが……DDPGではこの程度が限界なのか、学習環境が悪いのかまだ分かっていません。
おわりに
今年の2月ごろからなんとなく深層学習と強化学習を勉強し始め(当初はここまでやることになるとは思っていませんでした)、ようやくロボットを歩かせることができました。ずいぶん長い記事になってしまいましたが、これから深層学習や機械学習を勉強する方の助けになれば幸いです。
注釈
| 1. | ↑ | これは微分の連鎖律 (chain rule) を反映しています。 |
| 2. | ↑ | これも微分の連鎖律によるものです。実はノード e からは \dfrac{\partial e}{\partial c}\dfrac{\partial e}{\partial e} などが渡されていると考えても結果は変わらないので、場合分けは不要になります。 |
| 3. | ↑ | 実際のところ1つでは済みませんが、ノードから伸びる辺の数を定数とすれば高々定数個です。まあ実質1つです。 |
| 4. | ↑ | 実はこれが大変難しいです。強化学習の罠です。 |
| 5. | ↑ | 負の報酬は罰を表します。 |
| 6. | ↑ | 実際には、TD誤差による修正を繰り返したときに真のQ関数に常に収束するわけではなく、様々な条件が必要となります。 |
| 7. | ↑ | 実際のところはネットワークを繋げるのではなく、求めるべき勾配が「Critic Networkの出力を行動で微分したものと、行動をActor Networkのパラメータで微分したものの積の期待値である (Deterministic Policy Gradient Theorem) 」という定理に基づいて計算します。しかしこれはネットワークを繋げて微分したときに得られる値の期待値と等しくなります(定理の証明にもQ関数と方策関数の合成の微分を用いているので、根底にある考え方は合っているのではないかと思います)。 |
| 8. | ↑ | 後に同様のネットワークでの学習に成功しています。 |
