Deep Learning の初歩中の初歩(?)であるニューラルネットワーク (Neural Network) を自分で実装したときの覚え書きです。本当に何も知らない状態から始めたのでいろいろと大変でしたが、ひとまず形になったのでまとめておきたいと思います。
怪しい場所があればツッコミを入れていただけると筆者の勉強になります。
こうなった経緯ですが、「物理エンジンでロボットを学習して歩かせたい!」と思ったのがきっかけで強化学習について調べていて行きついたという感じです。ライブラリを使えば比較的簡単にできるのかもしれないですが、どうせなら自分で作りたいよねということで自作する流れになりました。
今のロボットはこんな感じです。歩けるようになるといいね。

Neural Network とは
Neural Network に関する解説は既に素晴らしいものがネット上に多く存在するのでここに書くのは気が引けるのですが、自分なりにまとめて書いてみることにします。
さて、一口に Neural Network と言っても色々あるようなのですが、基本的には「 n 次元入力を与えたときに m 次元出力を返す関数」です。
その中身は以下の図のようになっています。
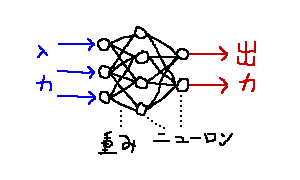
白丸のことをニューロン※1脳にあるニューロン細胞を模したものなので、「細胞」「形式ニューロン」と呼んだりもします。 (追記:形式ニューロンは活性化関数がステップ関数のもののみを指すようです)、ニューロン間を結ぶ黒い線を重みといいます。縦に並んでいるニューロンをまとめて「層」といい、入力を受け取るニューロンがいる層を入力層、結果を出力するニューロンがいる層を出力層、それ以外の層を隠れ層といいます。重みは隣り合った層にいるニューロンを繋ぐ場合が多いですが、RNN (Recurrent Neural Network) などそうでないモデルも存在します(ここでは扱いません)。
ニューロン
Neural Network は多数のニューロンが組み合わさってできたものです。まずは1つのニューロンがどのような働きをするかに注目しましょう。
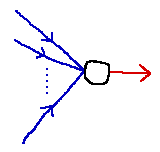
図のように、ニューロンは n 次元の入力 (y_1,y_2,\ldots,y_n) を受け取り、 1 次元の結果を出力します。各入力 i には重み w_i が設定されており、ニューロンはまず全ての入力の重み付き和を計算します。これを v とします。
\begin{aligned}
v=\sum_{i=1}^ny_iw_i+b
\end{aligned}
b はバイアスといい、入力によらない定数値を v に加える効果があります。
が、このバイアスが存在すると数学的な扱いが若干ややこしくなるため、「入力ニューロン中に常に 1 を出力するものを用意しておく」ことでこの b を抹殺します。
\begin{aligned}
v=\sum_{i=1}^ny_iw_i
\end{aligned}
b が消えました。
このままだとただの線型結合なのですが、ここで活性化関数 (Activation Function) と呼ばれる一般に非線形※2全てのニューロンの活性化関数を線形にしてしまうと、層を増やす意味が失われてしまいます。線形関数をいくら合成したところで線形関数のままであり、それは2層の Neural Network で等価なものが実現できるためです。
追記:全てのニューロンの活性化関数を線形にするとNNの出力は線形になりますが、砂時計型Neural Networkを用いて特徴抽出を行うなどの場合に、線形の活性化関数が多層のNeural Networkで用いられることもあるそうです。2層で同じ出力をするNeural Networkを作ることはできますが、このとき隠れ層の重みの情報は失われており、層を増やす意味がないわけではありません。(Xijanさんありがとうございました)な関数 \phi に v を適用し、その結果をニューロンの出力 y とします。この活性化関数は数学的に重要な意味を持っており、どのような活性化関数を使うかで Neural Network 全体の性能が大きく変わってきます。よく使われる活性化関数としては、シグモイド関数やHyperbolic Tangent、ランプ関数 (ReLU) などがあります。
\begin{aligned}
y=\phi(v)
\end{aligned}
このようにして得られた y は、また次の層にあるニューロンの入力として使われます。あるいは、このニューロンが出力層にあった場合は、 y が Neural Network の出力の一部となります。
Neural Network を学習させる
これで Neural Network を定義することができました。次に Neural Network を学習させることを考えます。学習とは簡単に言うと「ある入力に対し、望みの出力が得られるように重みを調整する」ことです。いま、入力 \vec x=(x_1,x_2,\ldots,x_n) が与えられたと仮定します※3入力データは複数あることがほとんどなのですが、ひとまず単一の入力に対する学習を考えます。。このときの出力を \vec y=(y_1,y_2,\ldots,y_m) とします。
ここで、損失関数 (Loss Function) と呼ばれる関数を定義します。損失関数 L は Neural Network の出力 \vec y を入力として実数を返します。Neural Network は、この損失関数の値 L(\vec y) が小さくなるように学習を進めます。損失関数を導入することで、「望みの出力を得る」というある種曖昧な目的を「損失関数の値を最小化する」という数学的な定義に置き換えることができます。
よく使われる損失関数としては、例えば二乗和誤差があります。これは、「望みの出力(=教師信号)」である \vec t=(t_1,t_2,\ldots,t_m) に対し、実際の出力 \vec y との差を2乗して和を取ったものです。
\begin{aligned}
L(\vec y)=\sum_{i=1}^m(y_i-t_i)^2
\end{aligned}
偏微分したときに出てくる係数 2 を相殺するため、これを 1/2 したものがよく使われるようです。
では、損失関数の値を小さくするためには具体的にどのように重みを調整すればよいのでしょうか。
そこで登場するのが最急降下法です。詳細は省きますが、最急降下法では全ての変数に対する関数の偏微分を求めて、「ある地点(=今の変数の値)で最も関数の値が速く減少する方向」に変数を動かすことを繰り返します。これを Neural Network に対して適用することで、損失関数が小さくなるように重みを変更することができます。
最急降下法を適用するためには、「Neural Network を使って入力から損失関数の値を求める部分」を「ニューロン間の重みを変数とした関数」と見なして、全ての重みについて偏微分しなくてはなりません。このために必要になるのがいわゆる誤差逆伝播法 (Backpropagation) と呼ばれる方法で、Neural Network の出力側から入力側に向かって順に微分係数を決定していきます。
誤差逆伝播法に関してはこちら 誤差逆伝播法のノート が非常に分かりやすくまとまっており、実装する上で参考になりました。
確率的勾配降下法
単一の入力に対する学習は先の方法で行うことができるのですが、一般に入力と教師信号は複数あり、複数の入力全体を見たときの損失関数の値を最小化する必要があります。そこで、入力全体に対する損失関数を「各入力に対する損失関数の値の平均※4平均ではなく総和で定義することもあります。」で定義することで、微分の線型性より、全体の損失関数に対する偏微分を各入力に対する損失関数の偏微分の平均で求めることができます。
この入力全体に対する損失関数を使って学習を繰り返すことで、Neural Network を入力全体に対して最適化させることができます。
しかし、学習分野によっては入力が最初から全て分かっていないということもあります。この場合先のような方法は使えないので、逐次的に学習を進めていくことが必要になります。ここで威力を発揮するのが確率的勾配降下法です。確率的勾配降下法では、特定の入力に対する学習を繰り返すのではなく、ランダムに出現する入力に対し一度ずつ学習を繰り返していきます。ここで「ランダムである」ということが重要であり、規則的に入力が出現する場合は学習がうまくいかないことがあります。例えばQ学習という強化学習の手法では、そのままでは入力が時系列に沿ったものになってしまうため、Neural Network を使う場合は入力をシャッフルする Experience Replay と呼ばれるテクニックが必要になります。
重みの初期値
初期状態、つまり「何も知らない」 Neural Network に対する重みの選択は慎重に行う必要があります( Math.random() * 2 - 1 で初期化、みたいなことをやったら学習が進まなくなりましたw)。良い方法としては、あるニューロンへの入力の重みを「平均 0 、分散 1/n ( n は入力の数) の正規分布」で決定するXavierの初期値、および分散をその2倍にしたHeの初期値※5Heの初期値は活性化関数として折れ線型の ReLU ( \max\{0,x\} ) を使う場合に有効なようです。が知られています。
自動微分
これは Neural Network に直接必要なものではないですが、自動微分を実装しておくと損失関数の偏微分を手作業でやる必要がなくなります。関数がデータ構造で表現できれば、微分の規則を当てはめて再帰的に計算するだけで簡単に求まりますので、詳細は省きます。
遊んでみた
以上の知識を基に、Neural Network を実装して色々学習させて遊んでみました。色が見えた方が視覚的に面白いということで、平面上の点を赤か青で色付けする分類問題を解かせてみることにしました。
入力は平面上の点の x,y 座標と定数の 1 、出力は \pm1 の範囲の値です。 -1 を青、 1 を赤としました。また、以下の動画では、学習過程を分かりやすくするために途中から学習を加速させています。
まずは一番単純な線形分離可能なケースです。

さすがに簡単だったようで、すぐに2色に分かれました。動画では境界がブレていますが、このまま学習を続けると左側(手本)とほぼ同じになります。
ならばと思い、お手本を縞模様にしてみました。

今度は少し難しかったようで、最初は分からずにチラチラしていますが、「縞模様があるらしい」というのが分かった途端にその部分の学習が急速に進みます。
では曲線はどうかということで、非対称な円を2つ配置してみました。

こちらも上手くいっています。これまでの実験で興味深いのが、重みの収束先が初期値からあまり離れていないという点です。ランダムに与えた初期値に対して、常にそれなりの精度をもつ局所解が近くに存在するというのは驚きました。
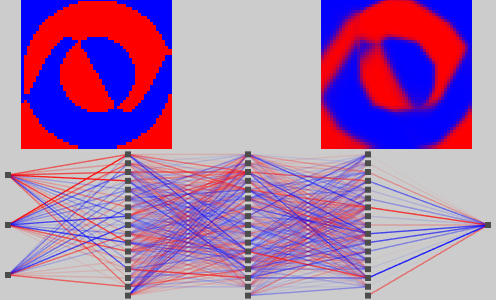
最後に、冒頭の画像の例です。

この程度の複雑さであれば、直線部分と曲線部分が交ざっていても問題なく学習できるようです。
今後
今後はこの Neural Network を使って強化学習ができると面白いなぁと思っています。当初の「ロボットを歩かせる」という目標はまだ遠いですが、長らく停滞していたゲーム制作と共に進められればと思います。
ソースコードについては、今は汚いのでアレですが、そのうちGitHubに上げるかもしれません。
注釈
| 1. | ↑ | 脳にあるニューロン細胞を模したものなので、「細胞」 |
| 2. | ↑ | 全てのニューロンの活性化関数を線形にしてしまうと、 追記:全てのニューロンの活性化関数を線形にするとNNの出力は線形になりますが、砂時計型Neural Networkを用いて特徴抽出を行うなどの場合に、線形の活性化関数が多層のNeural Networkで用いられることもあるそうです。2層で同じ出力をするNeural Networkを作ることはできますが、このとき隠れ層の重みの情報は失われており、層を増やす意味がないわけではありません。(Xijanさんありがとうございました) |
| 3. | ↑ | 入力データは複数あることがほとんどなのですが、ひとまず単一の入力に対する学習を考えます。 |
| 4. | ↑ | 平均ではなく総和で定義することもあります。 |
| 5. | ↑ | Heの初期値は活性化関数として折れ線型の ReLU ( \max\{0,x\} ) を使う場合に有効なようです。 |
はじめまして,楽しく読ませていただきました.
NNを実装して動かすには相応の知識と大変な手間がかかるものです.
こういった数値実験のそれもビジュアルなシェアは(他の多くの方が行っていようと)貴重なものです.
これからも更新楽しみにしております.物理エンジンでロボットの歩行が大目標とのことですが,あなたの腕の長いロボットのゲームをQ学習でプレイするということもできそうですね.
今回は非線型で無限に(*)複雑な函数を階層構造により近似できるという方向性のNNだったため少しそれるコメントで恐縮ですが,NNのような階層構造は次元縮約のためにもしばしば利用されます.砂時計型ニューラルネットワークやオートエンコーダと呼ばれるようなもので,盛んに研究されています.このような場合では活性化函数を線型(\phi(x)=x)にすることは全くないわけではなく,特に3層ですべての活性化函数を線型にしたものはreduced rank regression(縮小ランク回帰)と呼ばれる線型写像の低ランク回帰と等価なモデルになります.従いまして,活性化函数が線型な場合は2層のNNで等価なものが実現できるというのはこういった観点からは疑問です.学習・推測の結果得られる構造がただの線型回帰とは異なります.純粋に入出力に着目する場合は,おっしゃる通り合成しても線型なままです.
重箱の隅をつつくコメント失礼しました.
(*)実世界の函数は人間が作った(有限の)モデルとぴったり一致することはあまり期待されないという意味です.モデルが真を含む場合に何が起こるかを考察することは別の理由で意義がありますが割愛.
はじめまして、コメントいただきありがとうございます。
Q学習を利用したゲームプレイにも非常に興味があるのですが、取りうる行動が連続値になってしまうため(ロボットの歩行でも同じ問題が起こりますが…)いわゆるDeep Q-Networkでは学習できず、Actor-Criticモデルなどの方策に連続値が取れる手法を勉強中です。
活性化関数が全て線形の場合は2層のNNで等価なものが実現できると書いたのは入出力のみに注目した場合(すなわち、関数という意味において)であり、NNの学習結果から得られるものにつきましては、おっしゃる通り2層のものより有用なものがあるかと思います。NNとして等価であるという表現は確かに適切ではありませんでしたので、訂正させていただきます。
ご指摘ありがとうございました。また何かありましたらご教授いただければ幸いです。
初めまして.
NNを勉強していてこのブログにたどり着きました.
こういったビジュアル化をされている方が少なく、大変面白いと感じています.もしよろしければどのような手法で行なったのかお聞きしたいです.
初めまして。コメントありがとうございます。
可視化は今回はJavaScriptとCanvasを用いて行いました。このくらいのものを可視化しようとすると、グラフ描画ライブラリに投げるのが厳しくなってきますので、自分でプログラムを書いて描画するのがよいかと思います。動画はスクリーンをキャプチャできるソフトを使ってプログラムを実際に動かしながら撮影しました。
この、画像を色で分離するプログラムを教えて頂きたいのですが・・・全部。