FP11とStage3Dの登場で、一部の人たちの間で密かに人気が上がっている3Dですが、
これを機に3D表示には欠かせない変換行列について考えてみることにしました。
さて、3Dのライブラリなどを触っていると必ず出てくる変換行列ですが、
実際の所、よく分からずに使っている方も多いのではないでしょうか。
3D演算では、場合によってはフレーム毎に数万~数十万もの座標変換が発生するため、
効率よく座標変換できる行列が必要になります。
ここでは2Dの座標変換を例に、
それぞれの変換行列の成分がどんな意味を持つか考えてみます。
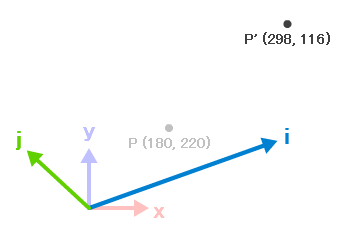
よく使われている座標系のひとつに、平面の xy 座標系があります。
x 軸を横方向、y 軸を縦方向として表すお馴染みの座標系です。
この座標系に、x 方向に a、y 方向に b だけ進んだ点 P があるとします。
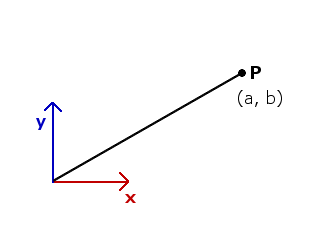
この点の位置は一般に (a, b) で表され、
座標軸のベクトルを使って ax + by と書くことができます。
ここでもう一つ座標系を用意します。この座標系は xy 座標系に対し少し回転していて、
それぞれの軸が i, j で表されます。
この座標系にも、i 方向に a、j 方向に b だけ進んだ点 P’ があるとします。
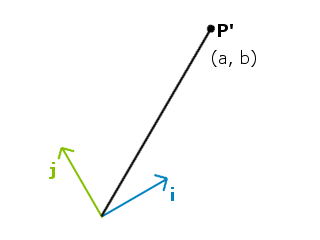
この点 P’ も、座標軸のベクトルを使って ai + bj と書くことができます。
では、点 P’ を xy 座標系で表すにはどうすればよいでしょうか。
この作業がいわゆる座標変換です。
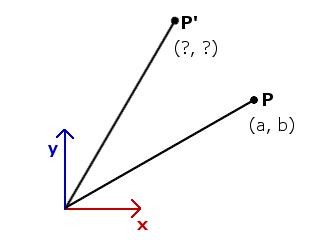
これは ij それぞれの x 成分と y 成分が分かれば難しくありません。
i = i1x + i2y
j = j1x + j2y
という具合に x 軸方向と y 軸方向に分解します。
後は前述の式 P' = ai + bj に代入すれば、
P' = a(i1x + i2y) + b(j1x + j2y)
P' = (a×i1 + b×j1)x + (a×i2 + b×j2)y
このようになります。なので、点 P’ は xy 座標系で
P' = (a×i1 + b×j1, a×i2 + b×j2)
と表すことができます。
ここでベクトルと行列の積を思い出すと、xy 座標系から ij 座標系に変換する行列は
※注1:行列の基本的な演算は検索すると大量にヒットするので省略します。
※注2:ベクトルは列ベクトルとします。行ベクトルの場合は合成順序を逆にして、
行列成分を転置(行と列を入れ替える)してください。
│i1, j1│
│i2, j2│
と表せます。
縦方向に変換先の座標軸の xyz 成分を並べただけですね。
これは変換先の座標軸が分かれば、代入だけで変換行列が作れることを意味します。
(作れなかったらそれはそれで困りますが…)
逆に言えば、変換行列を見れば、
その変換行列がどんな座標軸でできた座標系へ変換するのか分かるということになります。
3次元の変換行列も同様に3軸 i, j, k とその xyz 方向成分 1, 2, 3 を使えば、
│i1, j1, k1│
│i2, j2, k2│
│i3, j3, k3│
と表せます。
せっかくなので、座標軸から変換行列を作るサンプルを用意してみました。
i 軸と j 軸をドラッグして変換行列と点 P’ の変化を確かめてみてください。
ワカラナイ
すごく参考になりました!